


Next: Hierarchical Sorting
Up: Generating Hierarchical Clusterings
Previous: An Objective Function
As in COBWEB, AUTOCLASS [
Cheeseman et al., 1988],
and other systems [Anderson &
Matessa, 1991],
we will assume that clusters,  , are described probabilistically:
each variable value has an associated conditional probability,
, are described probabilistically:
each variable value has an associated conditional probability,
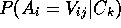 , which reflects the proportion of observations
in
, which reflects the proportion of observations
in 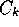 that exhibit the value,
that exhibit the value,  , along variable
, along variable  .
In fact, each variable value
is actually associated with the number of observations in the cluster
having that value; probabilities
are computed `on demand' for purposes of evaluation.
.
In fact, each variable value
is actually associated with the number of observations in the cluster
having that value; probabilities
are computed `on demand' for purposes of evaluation.

Figure 1: A probabilistic categorization tree.
Probabilistically-described clusters arranged in a tree
form a hierarchical
clustering known as a probabilistic categorization tree. Each set of
sibling clusters partitions the observations covered by the common parent.
There is a single root cluster, identical in structure to other
clusters, but covering all observations and containing frequency
information necessary to compute  's as required
by category utility. Figure 1 gives
an example of a probablistic categorization
tree (i.e., a hierarchical clustering) in which each node
is a cluster of observations summarized probabilistically.
Observations are at leaves and are described by three variables:
Size, Color, and Shape.
's as required
by category utility. Figure 1 gives
an example of a probablistic categorization
tree (i.e., a hierarchical clustering) in which each node
is a cluster of observations summarized probabilistically.
Observations are at leaves and are described by three variables:
Size, Color, and Shape.



Next: Hierarchical Sorting
Up: Generating Hierarchical Clusterings
Previous: An Objective Function
JAIR, 4
Douglas H. Fisher
Sat Mar 30 11:37:23 CST 1996
 , are described probabilistically:
each variable value has an associated conditional probability,
, are described probabilistically:
each variable value has an associated conditional probability,
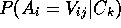 , which reflects the proportion of observations
in
, which reflects the proportion of observations
in 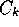 that exhibit the value,
that exhibit the value,  , along variable
, along variable  .
In fact, each variable value
is actually associated with the number of observations in the cluster
having that value; probabilities
are computed `on demand' for purposes of evaluation.
.
In fact, each variable value
is actually associated with the number of observations in the cluster
having that value; probabilities
are computed `on demand' for purposes of evaluation.




 's as required
by category utility. Figure
's as required
by category utility. Figure