


Next: Experiments with Validation
Up: Simplifying Hierarchical Clusterings
Previous: Simplifying Hierarchical Clusterings
Several authors [Fisher1987a; Cheeseman et al., 1988; Anderson &
Matessa, 1991]
motivate clustering as a means of improving
performance on a task akin to pattern completion,
where the error rate over completed patterns can be used to
`externally' judge the utility of a clustering. Given a probablistic
categorization tree of the type we have assumed, a new observation
with an unknown value for a variable can be classified down
the hierarchy using a small variation on the
hierarchical sorting procedure described earlier. Classification is terminated at a selected node (cluster) along the
classification path, and the variable value of highest probability
at that cluster is predicted as the unknown variable value of
the new observation. Naively, classification might always
terminate at a leaf (i.e., an observation), and the leaf's value
along the specified variable would be predicted as the variable value
of the new observation. Our use of a simple resampling strategy known as
holdout [Weiss &
Kulikowski, 1991] is motivated by the
fact that a variable might be better predicted at some internal
node in the classification path. The identification of
ideal-prediction frontiers for each variable
suggests a pruning strategy for hierarchical clusterings.
Classification is terminated at a selected node (cluster) along the
classification path, and the variable value of highest probability
at that cluster is predicted as the unknown variable value of
the new observation. Naively, classification might always
terminate at a leaf (i.e., an observation), and the leaf's value
along the specified variable would be predicted as the variable value
of the new observation. Our use of a simple resampling strategy known as
holdout [Weiss &
Kulikowski, 1991] is motivated by the
fact that a variable might be better predicted at some internal
node in the classification path. The identification of
ideal-prediction frontiers for each variable
suggests a pruning strategy for hierarchical clusterings.
Given a hierarchical clustering and a validation set
of observations, the validation set
is used to identify an appropriate
frontier of clusters for prediction of each variable.
Figure 4 illustrates that
the preferred frontiers of any two variables may differ, and clusters
within a frontier may be at different depths.
For each variable, 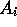 , the objects from the
validation set are each classified through the hierarchical
clustering with the value of variable
, the objects from the
validation set are each classified through the hierarchical
clustering with the value of variable 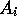 `masked' for purposes
of classification; at each cluster
encountered during classification
the observation's value for
`masked' for purposes
of classification; at each cluster
encountered during classification
the observation's value for  is compared to the most probable
value for
is compared to the most probable
value for  at the cluster; if they are the same, then
the observation's value would have been correctly predicted at the
cluster. A count of all such correct predictions for each variable
at a cluster is maintained. Following classification for all variables
over all observations of the validation set,
a preferred frontier for each variable is identified that
maximizes the number of correct counts for the variable.
This is a
simple, bottom-up procedure that insures that the number of correct counts
at a node on the variable's frontier is greater than or equal
to the sum of correct counts for the variable over each set
of mutually-exclusive, collectively-exhaustive descendents
of the node.
at the cluster; if they are the same, then
the observation's value would have been correctly predicted at the
cluster. A count of all such correct predictions for each variable
at a cluster is maintained. Following classification for all variables
over all observations of the validation set,
a preferred frontier for each variable is identified that
maximizes the number of correct counts for the variable.
This is a
simple, bottom-up procedure that insures that the number of correct counts
at a node on the variable's frontier is greater than or equal
to the sum of correct counts for the variable over each set
of mutually-exclusive, collectively-exhaustive descendents
of the node.

Figure 4: Frontiers for three variables in a hypothetical clustering.
From Fisher (1995). Figure reproduced with permission from
Proceedings of the First International Conference on Knowledge
Discovery in Data Mining, Copyright © 1995 American
Association for Artificial Intelligence.
Variable-specific frontiers enable a number
of pruning strategies. For example, a node that lies
below the frontier of every variable offers no apparent advantage
in terms of pattern-completion error rate; such a node probably
reflects no meaningful structure and it (and its descendents) may be
pruned. However, if an analyst is focusing attention on a subset
of the variables, then frontiers might be more flexibly exploited
for pruning.



Next: Experiments with Validation
Up: Simplifying Hierarchical Clusterings
Previous: Simplifying Hierarchical Clusterings
JAIR, 4
Douglas H. Fisher
Sat Mar 30 11:37:23 CST 1996
 Classification is terminated at a selected node (cluster) along the
classification path, and the variable value of highest probability
at that cluster is predicted as the unknown variable value of
the new observation. Naively, classification might always
terminate at a leaf (i.e., an observation), and the leaf's value
along the specified variable would be predicted as the variable value
of the new observation. Our use of a simple resampling strategy known as
holdout [Weiss &
Kulikowski, 1991] is motivated by the
fact that a variable might be better predicted at some internal
node in the classification path. The identification of
ideal-prediction frontiers for each variable
suggests a pruning strategy for hierarchical clusterings.
Classification is terminated at a selected node (cluster) along the
classification path, and the variable value of highest probability
at that cluster is predicted as the unknown variable value of
the new observation. Naively, classification might always
terminate at a leaf (i.e., an observation), and the leaf's value
along the specified variable would be predicted as the variable value
of the new observation. Our use of a simple resampling strategy known as
holdout [Weiss &
Kulikowski, 1991] is motivated by the
fact that a variable might be better predicted at some internal
node in the classification path. The identification of
ideal-prediction frontiers for each variable
suggests a pruning strategy for hierarchical clusterings.



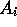 , the objects from the
validation set are each classified through the hierarchical
clustering with the value of variable
, the objects from the
validation set are each classified through the hierarchical
clustering with the value of variable 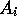 `masked' for purposes
of classification; at each cluster
encountered during classification
the observation's value for
`masked' for purposes
of classification; at each cluster
encountered during classification
the observation's value for  is compared to the most probable
value for
is compared to the most probable
value for  at the cluster; if they are the same, then
the observation's value would have been correctly predicted at the
cluster. A count of all such correct predictions for each variable
at a cluster is maintained. Following classification for all variables
over all observations of the validation set,
a preferred frontier for each variable is identified that
maximizes the number of correct counts for the variable.
This is a
simple, bottom-up procedure that insures that the number of correct counts
at a node on the variable's frontier is greater than or equal
to the sum of correct counts for the variable over each set
of mutually-exclusive, collectively-exhaustive descendents
of the node.
at the cluster; if they are the same, then
the observation's value would have been correctly predicted at the
cluster. A count of all such correct predictions for each variable
at a cluster is maintained. Following classification for all variables
over all observations of the validation set,
a preferred frontier for each variable is identified that
maximizes the number of correct counts for the variable.
This is a
simple, bottom-up procedure that insures that the number of correct counts
at a node on the variable's frontier is greater than or equal
to the sum of correct counts for the variable over each set
of mutually-exclusive, collectively-exhaustive descendents
of the node.
