


Next: Simplifying Hierarchical Clusterings
Up: Iterative Optimization
Previous: Comparisons between Iterative
Our experiments demonstrate the relative abilities of three iterative
optimization strategies, which have been coupled with the PU objective
function and hierarchical sorting to generate initial clusterings.
The reorder/resort optimization strategy of Section 3.1
makes most sense with sorting as the primary clustering
strategy, but the
other optimization techniques
are not strongly tied to a particular initial clustering strategy.
For example, hierarchical redistribution
can also be applied to hierarchical clusterings generated
by an agglomerative strategy [Duda &
Hart, 1973; Everitt, 1981; Fisher et al., 1992],
which uses a bottom-up procedure
to construct hierarchical clusterings by repeatedly `merging'
observations and resulting clusters until an all-inclusive
root cluster is generated. Agglomerative methods do not suffer
from ordering effects, but they are greedy algorithms, which are
susceptible to the limitations of local decision making generally,
and would thus likely benefit from iterative optimization.
In addition, all three optimization strategies can be applied regardless of
objective function. Nonetheless, the relative benefits of these methods
undoubtedly varies with objective function. For example,
the PU function has the undesirable characteristic that
it may, under very particular circumstances,
view two partitions that are very close in form as separated
by a `cliff' [Fisher, 1987b; Fisher et al., 1992].
Consider a partition of M observations
involving only two, roughly equal-sized clusters; its PU score has the form
 . If we create
a partition of three clusters by removing a single observation
from, say
. If we create
a partition of three clusters by removing a single observation
from, say 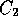 , and creating a new singleton cluster,
, and creating a new singleton cluster,  we have
we have  .
If M is relatively large,
.
If M is relatively large,
 will have a very small score due to the term,
will have a very small score due to the term, 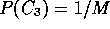 (see Section 2.1).
Because we are taking the average CU score of clusters,
the difference between
(see Section 2.1).
Because we are taking the average CU score of clusters,
the difference between  and
and
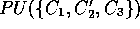 may be quite large, even though they
differ in the placement of only one observation. Thus,
limiting experiments to the PU function may exaggerate the general
advantage of hierarchical redistribution relative to
the other two optimization methods. This statement is
simultaneously a positive statement about the robustness
of hierarchical redistribution in the face of an objective function
with cliffs, and a negative statement about PU for
defining such discontinuities. Nonetheless, PU and variants
have been adopted in systems that fall within the
COBWEB family
[Gennari
et al., 1989; McKusick &
Thompson, 1990; Reich & Fenves,
1991,Iba & Gennari, 1991; McKusick &
Langley, 1991; Kilander,
1994; Ketterlin
et al., 1995; Biswas
et al., 1994].
Section 5.2 suggests some alternative objective
functions.
may be quite large, even though they
differ in the placement of only one observation. Thus,
limiting experiments to the PU function may exaggerate the general
advantage of hierarchical redistribution relative to
the other two optimization methods. This statement is
simultaneously a positive statement about the robustness
of hierarchical redistribution in the face of an objective function
with cliffs, and a negative statement about PU for
defining such discontinuities. Nonetheless, PU and variants
have been adopted in systems that fall within the
COBWEB family
[Gennari
et al., 1989; McKusick &
Thompson, 1990; Reich & Fenves,
1991,Iba & Gennari, 1991; McKusick &
Langley, 1991; Kilander,
1994; Ketterlin
et al., 1995; Biswas
et al., 1994].
Section 5.2 suggests some alternative objective
functions.
Beyond the nonoptimality of PU, our findings should
not be taken as the best that these strategies can do
when they are engineered for a particular clustering system.
We could introduce forms of randomization or systematic
variation to any of the three strategies.
For example, while Michalski and Stepp's seed-selection
methodology inspires reordering/resorting, Michalski and Stepp's
approach selects `border' observations when the selection
of `centroids' fails to improve clustering quality from
one iteration to the next; this is an example of the kind of
systematic variations that one might introduce in pursuit
of better clusterings. In contrast, AUTOCLASS may take large
heuristically-guided `jumps' away from a current clustering.
This approach might be, in fact, a somewhat less
systematic (but equally successful) variation on the macro-operator
theme that inspired hierarchical redistribution, and is similar to
HIERARCH's approach as well. SNOB [Wallace &
Dowe, 1994]
employs a variety of search operators, including operators similar
to COBWEB's merge and split (though without the same
restrictions on local application), random restart of the
clustering process with new seed observations, and `redistribution'
of observations. In fact, the user can program SNOB's search
strategy using these differing
primitive search operators.
In any case, systems such as CLUSTER/2, AUTOCLASS, and
SNOB do not simply `give up' when they fail
to improve clustering quality from one iteration to the next.
In fact, the user can program SNOB's search
strategy using these differing
primitive search operators.
In any case, systems such as CLUSTER/2, AUTOCLASS, and
SNOB do not simply `give up' when they fail
to improve clustering quality from one iteration to the next.
As SNOB illustrates, one or
more strategies might be combined to advantage.
As an additional example, Biswas et al. [1994]
adapt Fisher, Xu, and Zard's [1992]
dissimilarity ordering strategy
to preorder observations prior to clustering. After sorting using PU,
their ITERATE
system then applies iterative redistribution of single observations
using a category match measure by Fisher and Langley
[1990].
The combination of preordering and iterative redistribution
appears to yield good results in ITERATE. Our results
with reorder/resort suggest that preordering is primarily
responsible for quality benefits over a simple sort, but
the relative contribution of
ITERATE's redistribution operator is not certain since
it differs in some respects
from the redistribution technique described in this
paper. However, the use of three different
measures -- distance, PU, and category match -- during
clustering may be unnecessary and adds undesirable
coupling in the design of the clustering algorithm.
If, for example, one wants to experiment
with the merits of differing objective functions, it is undesirable
to worry about the `compatibility' of this function with two
other measures. In contrast, reordering/resorting generalizes
Fisher et al.'s [1992]
ordering strategy; this generalization and
the iterative redistribution strategy we describe assume no auxiliary
measures beyond the objective function.
In fact, as in Fisher [1987a; 1987b],
an evaluation of ITERATE's
clusterings is made using measures of variable value predictability
or
However, the use of three different
measures -- distance, PU, and category match -- during
clustering may be unnecessary and adds undesirable
coupling in the design of the clustering algorithm.
If, for example, one wants to experiment
with the merits of differing objective functions, it is undesirable
to worry about the `compatibility' of this function with two
other measures. In contrast, reordering/resorting generalizes
Fisher et al.'s [1992]
ordering strategy; this generalization and
the iterative redistribution strategy we describe assume no auxiliary
measures beyond the objective function.
In fact, as in Fisher [1987a; 1987b],
an evaluation of ITERATE's
clusterings is made using measures of variable value predictability
or 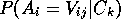 , predictiveness or
, predictiveness or 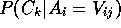 ,
and their product.
It is not clear that a system need exploit
several related, albeit different
measures during the generation and evaluation
of clusterings;
undoubtedly a single, carefully selected objective function can
be used exclusively during clustering.
,
and their product.
It is not clear that a system need exploit
several related, albeit different
measures during the generation and evaluation
of clusterings;
undoubtedly a single, carefully selected objective function can
be used exclusively during clustering.
Reordering/resorting and
iterative redistribution of single observations
could be combined in a manner similar to ITERATE's exploitation
of certain specializations of these procedures. Our results
suggest that reordering/resorting would put a clustering in
a good `ballpark', while iterative redistribution would subsequently make
modest refinements. We have not combined
strategies, but in a sense conducted the inverse of an `ablation' study,
by evaluating individual strategies in isolation.
In the limited number of domains explored in Section 3.4, however,
it appears difficult to better hierarchical redistribution.
Finally, our experiments applied various optimization
techniques after all data was sorted. It may be desirable
to apply the optimization procedures at intermittent points
during sorting. This may improve the quality of final clusterings
using reordering/resorting and redistribution of single observations,
as well as reduce the overall cost of constructing final optimized
clusterings using any of the methods, including hierarchical
redistribution, which already appears to do quite well on the quality
dimension. In fact, HIERARCH can be viewed as performing
something akin to a restricted form of hierarchical redistribution
after each observation. This is probably too extreme -- if iterative
optimization is performed too often, the resultant cost can
outweigh any savings gleaned by maintaining relatively
well optimized trees throughout the sorting process.
Utgoff [1994] makes a similar suggestion for intermittent
restructuring of decision trees during incremental, supervised induction.



Next: Simplifying Hierarchical Clusterings
Up: Iterative Optimization
Previous: Comparisons between Iterative
JAIR, 4
Douglas H. Fisher
Sat Mar 30 11:37:23 CST 1996
 . If we create
a partition of three clusters by removing a single observation
from, say
. If we create
a partition of three clusters by removing a single observation
from, say 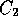 , and creating a new singleton cluster,
, and creating a new singleton cluster,  we have
we have  .
If M is relatively large,
.
If M is relatively large,
 will have a very small score due to the term,
will have a very small score due to the term, 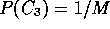 (see Section 2.1).
Because we are taking the average CU score of clusters,
the difference between
(see Section 2.1).
Because we are taking the average CU score of clusters,
the difference between  and
and
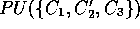 may be quite large, even though they
differ in the placement of only one observation. Thus,
limiting experiments to the PU function may exaggerate the general
advantage of hierarchical redistribution relative to
the other two optimization methods. This statement is
simultaneously a positive statement about the robustness
of hierarchical redistribution in the face of an objective function
with cliffs, and a negative statement about PU for
defining such discontinuities. Nonetheless, PU and variants
have been adopted in systems that fall within the
COBWEB family
[Gennari
et al., 1989; McKusick &
Thompson, 1990; Reich & Fenves,
1991,Iba & Gennari, 1991; McKusick &
Langley, 1991; Kilander,
1994; Ketterlin
et al., 1995; Biswas
et al., 1994].
Section 5.2 suggests some alternative objective
functions.
may be quite large, even though they
differ in the placement of only one observation. Thus,
limiting experiments to the PU function may exaggerate the general
advantage of hierarchical redistribution relative to
the other two optimization methods. This statement is
simultaneously a positive statement about the robustness
of hierarchical redistribution in the face of an objective function
with cliffs, and a negative statement about PU for
defining such discontinuities. Nonetheless, PU and variants
have been adopted in systems that fall within the
COBWEB family
[Gennari
et al., 1989; McKusick &
Thompson, 1990; Reich & Fenves,
1991,Iba & Gennari, 1991; McKusick &
Langley, 1991; Kilander,
1994; Ketterlin
et al., 1995; Biswas
et al., 1994].
Section 5.2 suggests some alternative objective
functions.




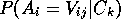 , predictiveness or
, predictiveness or 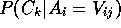 ,
and their product.
It is not clear that a system need exploit
several related, albeit different
measures during the generation and evaluation
of clusterings;
undoubtedly a single, carefully selected objective function can
be used exclusively during clustering.
,
and their product.
It is not clear that a system need exploit
several related, albeit different
measures during the generation and evaluation
of clusterings;
undoubtedly a single, carefully selected objective function can
be used exclusively during clustering.