Journal of Artificial Intelligence Research, 28 (2007) 453-515. Submitted 8/06; published 4/07

© 2007 AI Access Foundation and Morgan Kaufmann Publishers. All rights reserved.

Abstract Reasoning for Planning and Coordination

Bradley J. Clement
Jet Propulsion Laboratory, Mail Stop: 126-347
Pasadena, CA 91109 USA
brad.clement@jpl.nasa.gov

Edmund H. Durfee
Electrical Engineering and Computer Science Department
University of Michigan,Ann Arbor, MI 48109 USA
durfee@umich.edu

Anthony C. Barrett
Jet Propulsion Laboratory, Mail Stop: 126-347
Pasadena, CA 91109 USA
tony.barrett@jpl.nasa.gov

Abstract:

The judicious use of abstraction can help planning agents to identify key interactions between actions, and resolve them, without getting bogged down in details. However, ignoring the wrong details can lead agents into building plans that do not work, or into costly backtracking and replanning once overlooked interdependencies come to light. We claim that associating systematically-generated summary information with plans' abstract operators can ensure plan correctness, even for asynchronously-executed plans that must be coordinated across multiple agents, while still achieving valuable efficiency gains. In this paper, we formally characterize hierarchical plans whose actions have temporal extent, and describe a principled method for deriving summarized state and metric resource information for such actions. We provide sound and complete algorithms, along with heuristics, to exploit summary information during hierarchical refinement planning and plan coordination. Our analyses and experiments show that, under clearcut and reasonable conditions, using summary information can speed planning as much as doubly exponentially even for plans involving interacting subproblems.

1 Introduction

Abstraction is a powerful tool for solving large-scale planning and scheduling problems. By abstracting away less critical details when looking at a large problem, an agent can find an overall solution to the problem more easily. Then, with the skeleton of the overall solution in place, the agent can work additional details into the solution [Sacerdoti 1974, Tsuneto, Hendler, Nau, 1998]. Further, when interdependencies are fully resolved at abstract levels, then one or more agents can flesh out sub-pieces of the abstract solution into their full details independently (even in parallel) in a ``divide-and-conquer'' approach [Korf, 1987, Lansky, 1990, Knoblock, 1991].

Unfortunately, it is not always obvious how best to abstract large, complex problems to achieve these efficiency improvements. An agent solving a complicated, many-step planning problem, for example, might not be able to identify which of the details in earlier parts will be critical for later ones until after it has tried to generate plans or schedules and seen what interdependencies end up arising. Even worse, if multiple agents are trying to plan or schedule their activities in a shared environment, then unless they have a lot of prior knowledge about each other, it can be extremely difficult for one agent to anticipate which aspects of its own planned activities are likely to affect, and be affected by, other agents.

In this paper, we describe a strategy that balances the benefits and risks of abstraction in large-scale single-agent and multi-agent planning problems. Our approach avoids the danger of ignoring important details that can lead to incorrect plans (whose execution will fail due to overlooked interdependencies) or to substantial backtracking when abstract decisions cannot be consistently refined. Meanwhile, our approach still achieves many of the computational benefits of abstraction so long as one or more of a number of reasonable conditions (listed later) holds.

The key idea behind our strategy is to annotate each abstract operator in a plan hierarchy with summary information about all of its potential needs and effects under all of its potential refinements. While this might sound contrary to the purpose of abstraction as reducing the number of details, in fact we show that it strikes a good balance. Specifically, because all of the possibly relevant conditions and effects are modeled, the agent or agents that are reasoning with abstract operators can be absolutely sure that important details cannot be overlooked. However, because the summary information abstracts away details about under which refinement choices conditions and effects will or will not be manifested, and information about the relative timing of when conditions are needed and effects achieved, it still often results in an exponential reduction in information compared to a flat representation.

Based on the concept of summary information, this paper extends the prior work summarized below and in Section 8 to make the following contributions:

1.0.0.1 A formal model of hierarchical plans with temporal extent, and of their execution.

While many planning systems have sophisticated temporal models []<e.g.,>laborie:95,muscettola:94 and some additionally use hierarchical representations of alternative courses of action [Allen, Kautz, Pelavin, Tenenberg, 1991, Currie Tate, 1991, Chien, Knight, Stechert, Sherwood, Rabideau, 2000a, Castillo, Fdez-Olivares, García-Pérez, Palao, 2006], we know of no other work that extends the hierarchical task network (HTN) formalization [Erol, Hendler, Nau, 1994a, Erol, Nau, Hendler, 1994b] to include temporal extent. We need such a formalism in order to clarify the semantics of summary information and concurrently executing agents.

1.0.0.2 Algorithms for deriving summary information about propositional and metric resource conditions and effects, and for using such information to determine potential and definite interactions between abstract tasks.

We prove that our summarization techniques are guaranteed to correctly capture all of the conditions and effects associated with an abstract operator appropriately, augmented with modal information about whether conditions must or may hold and whether they hold during the entire operation or only for some of the time. Because summary information captures all conditions and effects, our algorithms can reason with operators at different levels of abstraction to predict and often resolve operator interactions without fully detailing task hierarchies, even for operators that are executing asynchronously at different agents.

1.0.0.3 Sound and complete algorithms for hierarchical refinement planning and centralized plan coordination for actions with temporal extent, supporting flexible plan execution systems.

An agent can reduce backtracking during planning by selectively interleaving the refinement of its plan with predicting and resolving potential interdependencies between its evolving plan and the plans that will be asynchronously executed by other agents. Other research has also found benefit in guiding refinement with conditions specified at higher levels in the plan hierarchy to guide refinement [Sacerdoti, 1974, Young, Pollack, Moore, 1994, Tsuneto, Hendler, Nau, 1998]. We show that our algorithms improve on these capabilities by exploiting the hierarchical structure using summary information to more efficiently converge on coordinated plans, which can then be further refined individually and in parallel by the participating agents.

This ability to coordinate at abstract levels rather than over detailed plans allows each of the agents to retain some local flexibility to refine its operators as best suits its current or expected circumstances without jeopardizing coordination or triggering new rounds of renegotiation. In this way, summary information supports robust execution systems such as PRS [Georgeff Lansky, 1986], UMPRS [Lee, Huber, Durfee, Kenny, 1994], RAPS [Firby, 1989], JAM [Huber, 1999], etc. that interleave the refinement of abstract plan operators with execution.

Our approach also extends plan coordination (plan merging) techniques [Georgeff, 1983, Lansky, 1990, Ephrati Rosenschein, 1994] by utilizing plan hierarchies and a more expressive temporal model. Prior techniques assume that actions are atomic, meaning that an action either executes before, after, or at exactly the same time as another. In contrast, we use interval point algebra [Vilain Kautz, 1986] to represent the possibility of several actions of one agent executing during the execution of one action of another agent. Because our algorithms can choose from alternative refinements in the HTN dynamically in the midst of plan coordination, they support interleaved local planning, multiagent coordination, and concurrent execution.

1.0.0.4 Search techniques and heuristics, including choose-fewest-threats-first (CFTF) and expand-most-threats-first (EMTF), that take advantage of summary information to prune the search space.

When interdependencies run more deeply in agents' plans, resolving them at abstract levels, if possible at all, can lead to unacceptable losses in parallel activity. Fortunately, even when agents need to delve into the details of their plans to tease out interdependencies, summary information can still enable exponential speedups by guiding decomposition and by pruning refinement choices. The search efficiency of using summary information comes from ignoring irrelevant information, which in a distributed planning system also reduces communication overhead exponentially.

1.0.0.5 Complexity analyses and experiments showing potential doubly-exponential speedups in refinement and local search planning/scheduling using summary information.

Our algorithms demonstrate that exploiting summary information to guide hierarchical planning and scheduling can achieve exponential speedups, and resolving interdependencies at abstract levels can improve the performance of plan coordination algorithms doubly exponentially. While others have shown that abstraction can exponentially reduce search space size [Korf, 1987, Knoblock, 1991] when subproblem independence properties hold, we show that our techniques lead to exponential improvements if any of these broader conditions hold for the problem:

• solutions can be found at abstract levels;
• the amount of summary information is less at higher levels than at lower levels; or
• choices of decompositions lead to varying numbers of plan threats.

When none of these conditions hold, we show that generating and using summary information provides no benefit and can increase computation and communication overhead. Thus, care must be taken when deciding to use summary information, though it has proven to be extremely worthwhile in the types of problem domains we have examined, an example of which we next describe.

1.1 Manufacturing Example

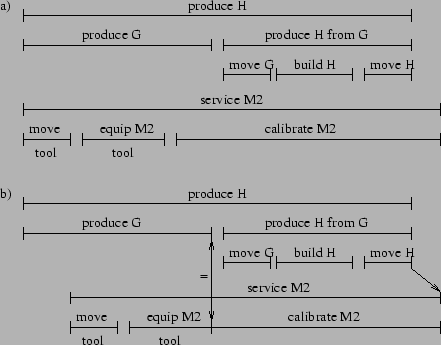
As a running example to motivate this work, consider a manufacturing plant where a production manager, a facilities manager, and an inventory manager each have their own goals with separately constructed hierarchical plans to achieve them. However, they still need to coordinate over the use of equipment, the availability of parts used in the manufacturing of other parts, storage for the parts, and the use of transports for moving parts around. The state of the factory is shown in Figure 1. In this domain, agents can produce parts using machines M1 and M2, service the machines with a tool, and move parts to and from the shipping dock and storage bins on the shop floor using transports. Initially, machines M1 and M2 are free for use, and the transports (transport1 and transport2), the tool, and all of the parts (A through E) shown in their storage locations are available.

Figure 1: A simple example of a manufacturing domain

The production manager is responsible for creating a part H using machines M1 and M2. Either M1 and M2 can consume parts A and B to produce G, and M2 can produce H from G. The production manager's hierarchical plan for manufacturing H involves using the transports to move the needed parts from storage to the input trays of the machines, manufacturing G and H, and transporting H back to storage. This plan is shown in Figure 2. Arcs through subplan branches mean that all subplans must be executed. Branches without arcs denote alternative choices to achieving the parent's goal. The decomposition of $produce\_G\_on\_M1$ is similar to that of $produce\_G\_on\_M2$.

Figure 2: The production manager's hierarchical plan

The facilities manager services each machine by equipping it with a tool and then calibrating it. The machines are unavailable for production while being serviced. The facilities manager's hierarchical plan branches into choices of servicing the machines in different orders and uses the transports for getting the tool from storage to the machines (Figure 3). The decomposition of $service\_M2M1$ is similar to that of $service\_M1M2$.

Figure 3: The facilities manager's hierarchical plan

The parts must be ``available'' on the space-limited shop floor in order for an agent to use them. Whenever an agent moves or uses a part, it becomes unavailable. The inventory manager's goal is just to move part C to the dock and move D and E into bins on the shop floor (shown in Figure 4).

Figure 4: The inventory manager's hierarchical plan

To accelerate the coordination of their plans, each factory manager can analyze his hierarchical plan to derive summary information on how each abstract plan operator can affect the world. This information includes the summary pre-, post-, and in-conditions that intuitively correspond to the externally required preconditions, externally effective postconditions, and the internally required conditions, respectively, of the plan based on its potential refinements. Summary conditions augment state conditions with modal information about whether the conditions must or may hold and when they are in effect. Examples are given at the end of Section 3.2.

Once summary information is computed, the production and inventory managers each could send this information for their top-level plan to the facilities manager. The facilities manager could then reason about the top-level summary information for each of their plans to determine that if the facilities manager serviced all of the machines before the production manager started producing parts, and the production manager finished before the inventory manager began moving parts on and off the dock, then all of their plans can be executed (refined) in any way, or $CanAnyWay$. Then the facilities manager could instruct the others to add communication actions to their plans so that they synchronize their actions appropriately.

This top-level solution maximizes robustness in that the choices in the production and facilities managers' plans are preserved, but the solution is inefficient because there is no concurrent activity--only one manager is executing its plan at any time. The production manager might not want to wait for the facilities manager to finish maintenance and could negotiate for a solution with more concurrency. In that case, the facilities manager could determine that they could not overlap their plans in any way without risking conflict ($\neg CanAnyWay$). However, the summary information could tell them that there might be some way to overlap their plans ($MightSomeWay$), suggesting that a search for a solution with more concurrency (at the cost of perhaps committing to specific refinement choices) has hope of success. In this case, the facilities manager could request the production manager for the summary information of each of $produce\_H$'s subplans, reason about the interactions of lower level actions in the same way, and find a way to synchronize the subplans for a more fine-grained solution where the plans are executed more concurrently. We give an algorithm for finding such solutions in Section 5.

1.2 Overview

We first formally define a model of a concurrent hierarchical plan, its execution, and its interactions (Section 2). Next, we describe summary information for propositional states and metric resources, mechanisms determining whether particular interactions must or may hold based on this information, and algorithms for deriving the information (Section 3). Built upon these algorithms are others for using summary information to determine whether a set of CHiPs must or might execute successfully under a set of ordering constraints (Section 4). These in turn are used within a sound and complete multilevel planning/coordination algorithm that employs search techniques and heuristics to efficiently navigate and prune the search space during refinement (Section 5). We then show how planning, scheduling, or coordinating at abstract levels can exponentially improve the performance of search and execution (Section 6). We provide experimental results demonstrating that the search techniques also greatly reduce the search for optimal solutions (Section 7). Finally, in Section 8 we differentiate our approach from related work that we did not mention elsewhere and conclude.

2 A Model of Hierarchical Plans and their Concurrent Execution

A representation of temporal extent in an HTN is important not only for modeling concurrently executing agents but also for performing abstract reasoning with summary information. If an agent is scheduling abstract actions and can only sequentially order them, it will be severely restricted in the kinds of solutions it can find. For example, the agent may prefer solutions with shorter makespans, and should seek plans with subthreads that can be carried out concurrently.

In this section we define concurrent hierarchical plans (CHiPs), how the state changes over time based on their executions, and concepts of success and failure of executions in a possible world, or history. Because we later define summary information and abstract plan interactions in terms of the definitions and semantics given in this section, the treatment here is fairly detailed (though for an even more comprehensive treatment, see [Clement, 2002]). However, we begin by summarizing the main concepts and notation introduced, to give the reader the basic gist.

2.1 Overview

A CHiP (or plan $p$) is mainly differentiated from an HTN by including in its definition inconditions, $in(p)$, (sometimes called ``during conditions'') that affect (or assert a condition on) the state just after the start time of $p$ ($t_s(p)$) and must hold throughout the duration of $p$. Preconditions ($pre(p)$) must hold at the start, and postconditions ($post(p)$) are asserted at the finish time of $p$ ($t_f(p)$). Metric resource ($res$) consumption ($usage(p,res)$) is instantaneous at the start time and, if the resource is defined as non-consumable, is instantaneously restored at the end. The decompositions of $p$ ($d(p)$) is in the style of $and$/$or$ tree, having either a partial ordering ($order(p)$) or a choice of child tasks that each can have their own conditions.

An execution $e$ of $p$ is an instantiation of its start time, end time, and decomposition. That is, an execution nails down exactly what is done and when. In order to reason about plan interactions, we can quantify over possible histories, where each history corresponds to a combination of possible executions of the concurrently-executing CHiPs for a partial ordering over their activities and in the context of an initial state. A run ($r(h,t)$) specifies the state at time $t$ for history $h$.

Achieve, clobber, and undo interactions are defined in terms of when the executions of some plans assert a positive literal $\ell$ or negative literal $\neg\ell$ relative to when $\ell$ is required by another plan's execution for a history. By looking at the literals achieved, clobbered, and undone in the set of executions in a history, we can identify the conditions that must hold prior to the executions in the history as external preconditions and those that must hold after all of the executions in the history as external postconditions.

The value of a metric resource at time $t$ ($r(res,h,t)$) is calculated by subtracting from the prior state value the usage of all plans that start executing at $t$ and (if non-consumable) adding back usages of all that end at $t$. An execution $e$ of $p$ fails if a condition that is required or asserted at time $t$ is not in the state $r(h,t)$ at $t$, or if the value of a resource ($r(res,h,t)$) used by the plan is over or under its limits during the execution.

In the remainder of this section, we give more careful, detailed descriptions of the concepts above, to ground these definitions in firm semantics; the more casual reader can skim over these details if desired. It is also important to note that, rather than starting from scratch, our formalization weaves together, and when necessary augments, appropriate aspects of other theories, including Allen's temporal plans allen:83b, Georgeff's theory for multiagent plans georgeff:84, and Fagin et al.'s theory for multiagent reasoning about knowledge RAK.

2.2 CHiPs

A concurrent hierarchical plan $p$ is a tuple $\langle pre$, $in$, $post$, $usage$, $type$, $subplans$, $order\rangle$. $pre(p)$, $in(p)$, and $post(p)$ are sets of literals ($v$ or $\neg v$ for some propositional variable $v$) representing the preconditions, inconditions, and postconditions defined for plan $p$.¹

We borrow an existing model of metric resources [Chien, Rabideu, Knight, Sherwood, Engelhardt, Mutz, Estlin, Smith, Fisher, Barrett, Stebbins, Tran, 2000b, Laborie Ghallab, 1995]. A plan's $usage$ is a function mapping from resource variables to an amount used. We write $usage(p,res)$ to indicate the amount $p$ uses of resource $res$ and sometimes treat $usage(p)$ as a set of pairs $(res, amount)$. A metric resource $res$ is a tuple $\langle min\_value$, $max\_value$, $type\rangle$. The min and max values can be integer or real values representing bounds on the capacity or amount available. The $type$ of the resource is either consumable or non-consumable. For example, fuel and battery energy are consumable resources because, after use, they are depleted by some amount. A non-consumable resource is available after use (e.g. vehicles, computers, power).

Domain modelers typically only specify state conditions and resource usage for primitive actions in a hierarchy. Thus, the conditions and usage of a CHiP are used to derive summary conditions, as we describe in Section 3.4, so that algorithms can reason about any action in the hierarchy. In order to reason about plan hierarchies as and/or trees of actions, the $type$ of plan $p$, or $type(p)$, is given a value of either $primitive$, $and$, or $or$. An $and$ plan is a non-primitive plan that is accomplished by carrying out all of its subplans. An $or$ plan is a non-primitive plan that is accomplished by carrying out exactly one of its subplans. So, $subplans$ is a set of plans, and a $primitive$ plan's $subplans$ is the empty set. $order(p)$ is only defined for an $and$ plan $p$ and is a consistent set of temporal relations [Allen, 1983] over pairs of subplans. Plans left unordered with respect to each other are interpreted to potentially execute concurrently.

The decomposition of a CHiP is in the same style as that of an HTN as described by erol:94. An $and$ plan is a task network, and an $or$ plan is an extra construct representing a set of all methods that accomplish the same goal or compound task. A network of tasks corresponds to the subplans of a plan.

For the example in Figure 2, the production manager's highest level plan $produce\_H$ (Figure 2) is the tuple $$\langle\{\}, \{\}, \{\}, \{\}, and, \{produce\_G, produce\_H\_from\_G\}, \{before(0, 1) \}\rangle.$$ In $before$(0,1), 0 and 1 are indices of the subplans in the decomposition referring to $produce\_G$ and $produce\_H\_from\_G$ respectively. There are no conditions defined because $produce\_H$ can rely on the conditions defined for the primitive plans in its refinement. The plan for moving part A from bin1 to the first input tray of M1 using transport1 is the tuple $$\langle\{ \}, \{ \}, \{ \}, \{\}, and, \{start\_move, finish\_move\}, \{meets(0, 1)\}\rangle.$$ This plan decomposes into two half moves which help capture important intermediate effects. The parent orders its children with the $meets$ relation to bind them together into a single move. The $start\_move$ plan is $$\begin{array}{@{}l@{}l} \langle & \{at(A,bin1), available(A)... ...tray1) \},\\ & \{\}, primitive, \{\}, \{\}\rangle. \end{array}$$ The $finish\_move$ plan is $$\begin{array}{@{}l@{}l} \langle & \{\neg at(A, bin1), \neg a... ...tray1)\}, \\ & \{\}, primitive, \{\}, \{\}\rangle. \end{array}$$ We split the move plan into these two parts in order to ensure that no other action that executes concurrently with this one can use transport1, part A, or the input tray to M1. It would be incorrect to instead specify $\neg free$(transport1) as an incondition to a single plan because another agent could, for instance, use transport1 at the same time because its $\neg free$(transport1) incondition would agree with the $\neg free$(transport1) incondition of this move action. However, the specification here is still insufficient since two pairs of ($start\_move$, $finish\_move$) actions could start and end at the same time without conflict. We can get around this by only allowing the planner to reason about the $move\_plan$ and its parent plans, in effect, hiding the transition between the start and finish actions. So, by representing the transition from $free$ to $\neg free$ without knowing when that transition will take place the modeler ensures that another move plan that tries to use transport1 concurrently with this one will cause a conflict.²

A postcondition is required for each incondition to specify whether the incondition changes. This clarifies the semantics of inconditions as conditions that hold only during plan execution whether because they are caused by the action or because they are necessary conditions for successful execution.

2.3 Executions

Informally, an execution of a CHiP is recursively defined as an instance of a decomposition and an ordering of its subplans' executions. Intuitively, when executing a plan, an agent chooses the plan's start time and how it is refined, determining at what points in time its conditions must hold, and then witnesses a finish time. The formalism helps us reason about the outcomes of different ways to execute a group of plans, describe state transitions, and define summary information.

An execution $e$ of CHiP $p$ is a tuple $\langle d, t_s, t_f\rangle$. $t_s(e)$ and $t_f(e)$ are positive, non-zero real numbers representing the start and finish times of execution $e$, and $t_s < t_f$. Thus, instantaneous actions are not explicitly represented. $d(e)$ is a set of subplan executions representing the decomposition of plan $p$ under this execution $e$. Specifically, if $p$ is an $and$ plan, then it contains exactly one execution from each of the subplans; if it is an $or$ plan, then it contains only one execution of one of the subplans; and it is empty if it is $primitive$. In addition, for all subplan executions, $e'\in d$, $t_s(e')$ and $t_f(e')$ must be consistent with the relations specified in $order(p)$. Also, the first subplan(s) to start must start at the same time as $p$, $t_s(e')=t_s(e)$, and the last subplan(s) to finish must finish at the same time as $p$, $t_f(e')=t_f(e)$. The possible executions of a plan $p$ is the set $\mathcal{E}$$(p)$ that includes all possible instantiations of an execution of $p$, meaning all possible values of the tuple $\langle d, t_s, t_f\rangle$, obeying the rules just stated.

For the example in Section 1.1, an execution for the production manager's top-level plan $produce\_H$ would be some $e\in\mathcal{E}$$(produce\_H)$. $e$ might be $\langle\{e_1$, $e_2\}$, 2.0, 9.0 $\rangle$ where $e_1\in\mathcal{E}$$(produce\_G)$, and $e_2\in\mathcal{E}$$(produce\_H\_from\_G)$. This means that the execution of $produce\_H$ begins at time 2.0 and ends at time 9.0.

For convenience, the subexecutions of an execution $e$, or $subex(e)$, is defined recursively as the set of subplan executions in $e$'s decomposition unioned with their subexecutions.

2.4 Histories and Runs

An agent reasoning about summary information to make planning decisions at abstract levels needs to first be able to reason about CHiPs. In this section we complete the semantics of CHiPs by describing how they affect the state over time. Because an agent can execute a plan in many different ways and in different contexts, we need to be able to quantify over possible worlds (or histories) where agents fulfill their plans in different ways. After defining a history, we define a run as the transformation of state over time as a result of the history of executions. The formalization of histories and runs follows closely to that of RAK in describing multiagent execution.

A state of a world, $s$, is a truth assignment to a set of propositions, each representing an aspect of the environment. We will refer to the state as the set of true propositional variables. A history, $h$, is a tuple $\langle E, s_I\rangle$. $E$ is the set of all plan executions of all agents occurring in $h$, and $s_I$ is the initial state of $h$ before any plan begins executing. So, a history $h$ is a hypothetical world that begins with $s_I$ as the initial state and where only executions in $E(h)$ occur. In particular, a history for the manufacturing domain might have an initial state as shown in Figure 1 where all parts and machines are available, and both transports are free. The set of executions $E$ would contain the execution of $produce\_H$, $maintenance$, $move\_parts$, and their subexecutions.

A run, $r$, is a function mapping a history and time point to states. It gives a complete description of how the state of the world evolves over time, where time ranges over the positive real numbers.

Axiom 1   $$r(h,0) = s_I$$

Axiom 2   $$\begin{array}{@{}l@{}l@{}l} v \in r(h,t>0) \Leftrightarrow &... ...(\neg v \in post(p') \wedge t_f(e_{p'}) = t)) \par \end{array}$$

Axiom 1 states that the world is in the initial state at time zero. Axiom 2 states that a predicate $v$ is true at time $t$ if it was already true beforehand, or a plan asserts $v$ with an incondition or postcondition at $t$, but (in either case) no plan asserts $\neg v$ at $t$. If a plan starts at $t$, then its inconditions are asserted right after the start, $t+\epsilon$, where $\epsilon$ is a small positive real number. Axiom 2 also indicates that both inconditions and postconditions are effects.

The state of a resource is a level value (integer or real). For consumable resource usage, a task that depletes a resource is modeled to instantaneously deplete the resource (subtract $usage$ from the current state) at the start of the task by the full amount. For non-consumable resource usage, a task also depletes the usage amount at the start of the task, but the usage is restored (added back to the resource state) at the end of execution. A task can replenish a resource by having a negative $usage$. We will refer to the level of a resource $res$ at time $t$ in a history $h$ as $r(res,h,t)$. Axioms 3 and 4 describe these calculations for consumable and non-consumable resources, respectively.

Axiom 3   $$\begin{array}{@{}l@{}l@{}l} r(consumable\_res,h,t) = r(consu... ..._{e_p\in E(h), t_s(e_p)=t} usage(p,consumable\_res) \end{array}$$

Axiom 4   $$\begin{array}{@{}l@{}l@{}l} r(nonconsumable\_res,h,t) = &r(n... ..._p\in E(h), t_f(e_p)=t} usage(p,nonconsumable\_res) \end{array}$$

Now that we have described how CHiPs change the state, we can specify the conditions under which an execution succeeds or fails. As stated formally in Definition 1, an execution succeeds if: the plan's preconditions are met at the start; the postconditions are met at the end; the inconditions are met throughout the duration (not including the start or end); all used resources stay within their value limits throughout the duration; and all executions in the decomposition succeed. Otherwise, the execution fails.

Definition 1   $$\begin{array}{@{}l@{}l} succeeds(e_p, h) \equiv &pre(p) \sub... ...nd{array} \\ &\forall e \in d(e_p), succeeds(e,h) \end{array}$$

2.5 Asserting, Clobbering, Achieving, and Undoing

Conventional planning literature often speaks of clobbering and achieving preconditions of plans [Weld, 1994]. In CHiPs, these notions are slightly different since inconditions can clobber and be clobbered, as seen in the previous section. Formalizing these concepts and another, undoing postconditions, helps us define summary conditions (in Section 3.2). However, it will be convenient to define first what it means to assert a condition. Figure 5 gives examples of executions involved in these interactions, and we define these terms as follows:

Definition 2   $$\begin{array}{@{}l@{}l@{}l} asserts(e_p,\ell,t,h) \equiv &(&... ...ge t = t_f(e_p)) \wedge \\ &(&r(t,h) \vdash \ell) \end{array}$$

Definition 2 states that an execution $e_p$ in a history $h$ asserts a literal at time $t$ if that literal is an effect of $p$ that holds in the state at $t$. Note that that from this point on, beginning in Definition 3, we use brackets [ ] as a shorthand when defining similar terms and procedures. For example, saying ``[$a$, $b$] implies [$c$, $d$]'' means $a$ implies $c$, and $b$ implies $d$. This shorthand will help us avoid repetition, at the cost of slightly more difficult parsing.

Definition 3   $$\begin{array}{@{}l@{}l@{}l} [ach&ieves,clobbers] \_precondit... ...{p''},\neg\ell,t'',h)) \wedge t<t''\leq t_s(e_{p'}) \end{array}$$

Definition 4   $$\begin{array}{@{}l@{}l@{}l} clob&bers\_[in,post]condition(e_... ...] \wedge [t_s(e_{p'})<t<t_s(e_{p'}), t=t_f(e_{p'})] \end{array}$$

Definition 5   $$\begin{array}{@{}l@{}l@{}l} undo&es(e_p,\ell,e_{p'},t,h) \eq... ...'},\neg\ell,t'',h)) \wedge t_f(e_{p'}) \leq t'' < t \end{array}$$

So, an execution achieves or clobbers a precondition if it is the last (or one of the last) to assert the condition or its negation (respectively) before it is required. Likewise, an execution undoes a postcondition if it is the first (or one of the first) to assert the negation of the condition after the condition is asserted. An execution $e$ clobbers an incondition or postcondition of $e'$ if $e$ asserts the negation of the condition during or at the end (respectively) of $e'$. Achieving effects (inconditions and postconditions) does not make sense for this formalism, so it is not defined. Figure 5 shows different ways an execution $e$ achieves, clobbers, and undoes an execution $e'$. $\ell$ and $\neg\ell$ point to where they are asserted or required to be met.

Figure 5: Interval interactions of plan steps

2.6 External Conditions

As recognized by tsuneto:98, external conditions are important for reasoning about potential refinements of abstract plans. Although the basic idea is the same, we define them a little differently and call them external preconditions to differentiate them from other conditions that we call external postconditions. Intuitively, an external precondition of a group of partially ordered plans is a precondition of one of the plans that is not achieved by another in the group and must be met external to the group. External postconditions, similarly, are those that are not undone by plans in the group and are net effects of the group. Definition 6 states that $\ell$ is an external [pre, post]condition of an execution $e_p$ if $\ell$ is a [pre, post]condition of a subplan for which it is not [achieved, undone] by some other subplan.

Definition 6   $$\begin{array}{@{}l@{}l@{}l} exte&rnal\_[pre,post]condition(\... ...st]condition(e_{p''}, \ell, e_{p'},t,h)) \end{array}\end{array}$$

For the example in Figure 2, $available(G)$ is not an external precondition because, although G must exist to produce H, G is supplied by the execution of the $produce\_G$ plan. Thus, $available(G)$ is met internally, making $available(G)$ an internal condition. $available(M1)$ is an external precondition, an internal condition, and an external postcondition because it is needed externally and internally; it is an effect of $produce\_G\_on\_M1$ which releases M1 when it is finished; and no other plan in the decomposition undoes this effect.

3 Plan Summary Information

Summary information can be used to find abstract solutions that are guaranteed to succeed no matter how they are refined because the information describes all potential conditions of the underlying decomposition. Thus, some commitments to particular plan choices, whether for a single agent or between agents, can be made based on summary information without worrying that deeper details lurk beneath that will doom the commitments. While HTN planners have used abstract conditions to guide search []<e.g.,>sacerdoti:74,tsuneto:98, they rely on a user-defined subset of constraints that can only help detect some potential conflicts. In contrast, summary information can be used to identify all potential conflicts.

Having the formalisms of the previous section, we can now define summary information and describe a method for computing it for non-primitive plans (in Section 3.4). Because there are many detailed definitions and algorithms in this section, we follow the same structure here as in the previous section, where we first give a more informal overview of the key concepts and notation, into which we then subsequently delve more systematically.

3.1 Overview

The summary information of plan $p$ consists of summary pre-, in-, and postconditions ($pre_{sum}(p)$, $in_{sum}(p)$, $post_{sum}(p)$), summary resource usage ($usage_{sum}(p,res)$) for each resource $res$, and whether the plan can be executed in any way successfully ($consistent$).

A summary condition (whether pre, post, or in) specifies not only a positive or negated literal, but additional modal information. Each summary condition has an associated $existence$, whose value is either $must$ or $may$ depending on whether it must hold for all possible decompositions of the abstract operator or just may hold depending on which decomposition is chosen. The $timing$ of a summary condition is either $first$, $last$, $always$, or $sometimes$, specifying when the condition must hold in the plan's interval of execution. A plan $p_1$ must [achieve, clobber] summary precondition $c_2$ of $p_2$ if the execution of $p_1$ (or that of any plan with the same summary information) would [achieve, clobber] a condition summarized by $c_2$ (or any plan with the same summary information as $p_2$).

The algorithm for deriving summary conditions for plan $p$ takes as input the summary conditions of the immediate subplans of $p$ and the conditions defined for the CHiP $p$. The pre-, in-, and postconditions of $p$ become must first, must always, and must last summary conditions, respectively. The algorithm retains the existence and timing of subplan summary conditions in the parent depending on whether the conditions are achieved, clobbered, or undone by siblings, whether the decomposition is $and$ or $or$, whether the subplan is ordered first or last, and whether all subplans share the same condition. Subplan first, always, and last conditions can become sometimes conditions in the parent. The parent is computed as $consistent$ as long as all subplans are $consistent$, no subplan may clobber a summary condition of another, and summarized resources do not violate limits.

We represent summary resource usage as three value ranges, $\langle local\_min$, $local\_max$, $persist \rangle$, where the resource's local usage occurs within the task's execution, and the persistent usage represents the usage that lasts after the task terminates for depletable resources. The summarization algorithm for an abstract task takes the summary resource usages of its subtasks, considers all legal orderings of the subtasks, and all possible usages for all subintervals within the interval of the abstract task, to build multiple usage profiles. These profiles are combined with algorithms for computing parallel, sequential, and disjunctive usages to give the summary usage of the parent task.

3.2 Summary Conditions

The summary information for a plan $p$, $p_{sum}$, is a tuple $\langle pre_{sum}$, $in_{sum}$, $post_{sum}$, $usage_{sum}$, $consistent\rangle$, whose members are sets of summary conditions, summarized resource usage, and a $consistent$ flag indicating whether the plan will execute consistently internally. $pre_{sum}(p)$ and $post_{sum}(p)$ are summary pre- and postconditions, which are the external pre- and postconditions of $p$, respectively. The summary inconditions of $p$, $in_{sum}(p)$, contain all conditions that must hold within some execution of $p$ for it to be successful. A condition $c$ in one of these sets is a tuple $\langle\ell,existence, timing\rangle$. $\ell(c)$ is the literal of $c$. The $existence$ of $c$ can be $must$ or $may$. If $existence(c)=must$, then $c$ is called a $must$ condition because $\ell$ must hold for every successful plan execution. For convenience we usually write $must(c)$. $c$ is a $may$ condition ($may(c)$ is $true$) if $\ell(c)$ must hold for some successful execution.

The $timing$ of a summary condition $c$ can either be $always$, $sometimes$, $first$, or $last$. $timing(c)$ is $always$ for $c\in in_{sum}$ if $\ell(c)$ is an incondition that must hold throughout all potential executions of $p$ ($\ell$ holds always); otherwise, $timing(c)=sometimes$ meaning $\ell(c)$ holds at one point, at least, within an execution of $p$. So, an $always$ condition is $must$, and we do not define $may$ $always$ inconditions because whether it is $may$ because of existence or timing, it is not significantly different from $may$ $sometimes$ in how a planner reasons about it. Whether a condition is $may$ $always$ (however defined) or $may$ $sometimes$, another plan can only have a $may$ $clobber$ relationship with the condition (as defined in Section 3.3). Note also that the incondition of a CHiP has the restricted meaning of a $must$ $always$ summary incondition. The $timing$ is $first$ for $c\in pre_{sum}$ if $\ell(c)$ holds at the beginning of an execution of $p$; otherwise, $timing=sometimes$. Similarly, $timing$ is $last$ for $c\in post_{sum}$ if $\ell(c)$ is asserted at the end of a successful execution of $p$; otherwise, it is $sometimes$. Although $existence$ and $timing$ syntactically only take one value, semantically $must(c)\Rightarrow may(c)$, and $always(c)\Rightarrow sometimes(c)$.

We considered using modal logic operators to describe these concepts. While a mix of existing temporal logic and dynamic logic [Pratt, 1976] notation could be forced to work, we found that using our own terminology made definitions much simpler. We discuss this more at the end of Section 8.

Definitions 7, 8, and 9 give the formal semantics of $existence$ and $timing$ for a few representative condition types. Summary conditions of a plan are defined recursively in that they depend on the summary conditions of the plan's immediate subplans instead of its complete decomposition. Because a single description of summary information could represent many different plan hierarchies, we quantify over plans $p'$, whose subplans have the same summary information as those of the plan $p$ being summarized. We could have defined the existence and timing properties of conditions based on the entire hierarchy, but in doing so, deriving summary conditions would be as expensive as solving the planning problem, and one of the main purposes of summary information is to reduce the computation of the planning problem. The reason why it would be so expensive is that in the worst case all legal orderings of all plan steps must be explored to determine whether a condition is $must$ or $may$. We will discuss an example of this at the end of this subsection.

Definition 7   $$\begin{array}{@{}l@{}l@{}l} [mu&st,may]\_first\_precondition... ...}) \wedge \ell \in pre(p'') \end{array} \end{array}\end{array}$$

Definition 8   $$\begin{array}{@{}l@{}l@{}l} must&\_always\_incondition(\ell,... ...{p''}) \wedge \ell\in in(p'') \end{array}\end{array}\end{array}$$

Definition 9   $$\begin{array}{@{}l@{}l@{}l} [mus&t,may]\_sometimes\_incondit... ... \ell\in post(p'') \end{array}\end{array}\end{array}\end{array}$$

Definition 7 states that a $first$ precondition of $p$ is an external precondition that is always required at the beginning of the execution of any $p'$ that has the same conditions as $p$ and the same summary information and ordering for its subplans as $p$. A last postcondition is always asserted at the end of the execution (substitute ``pre'' with ``post'' and $t_s$ with $t_f$ in the last two lines of Definition 7). A [must,may] sometimes precondition is a [must,may] external precondition that is not a $first$ precondition. A sometimes postcondition is defined similarly. Definition 8 states that a literal $\ell$ is a $must$, $always$ incondition of a plan $p$ if at any time during any isolated execution of any $p'$ with the same summary information as $p$, some executing plan $p''$ has incondition $\ell$. Definition 9 states that a [must, may] sometimes incondition of plan $p$ is a condition that is required during [any, some] execution of [any, some] plan $p'$ that has the same summary information and ordering for its subplans as $p$.

The $consistent$ flag is a boolean indicating whether the plan (or any plan with the same summary information and ordering for subplans) would execute successfully no matter how it was decomposed and no matter when its subplans were executed. Definition 10 says that all possible executions will succeed for a consistent plan. This is very similar to the $CanAnyWay$ relation that will be defined in Section 4. We do not include whether the plan will definitely not succeed in the summary information because it requires an exponential computation to see whether all conflicts in the subplans can be resolved. This computation can wait to be done during planning after summary information is fully derived.

Definition 10   $$\begin{array}{@{}l@{}l@{}l} cons&istent(p) \equiv \\ &\for... ...p'} \in \mathcal{E}(p'), e_{p'} succeeds \end{array}\end{array}$$

We show a subset of the summary conditions for the production manager's top-level plan (of Figure 2) below. Following each literal are modal tags for $existence$ and $timing$ information. ``Mu'' is $must$; ``Ma'' is $may$; ``F'' is $first$; ``L'' is $last$; ``S'' is $sometimes$; and ``A'' is $always$.

Production manager's $produce\_H$ plan:
Summary preconditions:
available(A)MuF, available(M1)MaS, available(M2)MaS
Summary inconditions:
$\neg$available(A)MuS, available(M1)MaS, available(M2)MuS, available(G)MuS,
available(A)MuS, $\neg$available(M1)MaS, $\neg$available(M2)MuS, $\neg$available(G)MuS,
available(H)MuS, $\neg$available(H)MuS
Summary postconditions:
$\neg$available(A)MuS, available(M1)MaS, available(M2)MuS, $\neg$available(G)MuS,
available(H)MuL

The $available(M1)$ summary precondition is a $may$ condition because the production manager may end up not using M1 if it chooses to use M2 instead to produce G. $available(A)$ is a $first$ summary precondition because part A must be used at the beginning of execution when it is transported to one of the machines. Because the machines are needed sometime after the parts are transported, they are sometimes (and not first) conditions: they are needed at some point in time after the beginning of execution.

Because the production manager may use M1 to produce G, $\neg available(M1)$ is a summary incondition of $produce\_H$. Having both $available(M1)$ and $\neg available(M1)$ as inconditions is consistent because they are $sometimes$ conditions, implying that they hold at different times during the plan's execution. In contrast, these conditions would conflict if they were both $must$ and $always$ (meaning that they must always hold throughout every possible execution of the plan).

The summary condition $\neg available(A)$ is a $must$ postcondition of the top-level plan because A will definitely be consumed by $make\_G$ and is not produced by some other plan in the decomposition of $produce\_H\_from\_G$. Even though $available(G)$ is an effect of $produce\_G$, it is not an external postcondition of $produce\_H$ because it is undone by $produce\_H\_from\_G$, which consumes G to make H. $available(H)$ is a $last$ summary postcondition because the production manager releases H at the very end of execution. $available(M2)$ is not $last$ because the manager finishes using M2 before moving H into storage.

Notice that $available(M2)$ is a $may$ summary precondition. However, no matter how the hierarchy is decomposed, M2 must be used to produce H, so $available(M2)$ must be established externally to the production manager's plan. Because summary information is defined in terms of the summary information of the immediate subplans, in the subplans of $produce\_H$, we only see that $produce\_G$ has an $available(M2)MaS$ precondition and an $available(M2)MaS$ postcondition that would achieve the $available(M2)MuF$ precondition of $produce\_H\_from\_G$. This summary information does not tell us that the precondition of $produce\_G$ exists only when the postcondition exists, a necessary condition to determine that the derived precondition of $produce\_H$ is a $must$ condition. Thus, it is $may$. If we augmented summary information with which subsets of conditions existed together, hunting through combinations and temporal orderings of condition subsets among subplans to derive summary conditions would basically be an adaptation of an HTN planning algorithm, which summary information is intended to improve. Instead, we derive summary information in polynomial time and then use it to improve HTN planning exponentially as we explain in Section 6. This is the tradeoff we made at the beginning of this section in defining summary conditions in terms of just the immediate subplans instead of the entire hierarchy. Abstraction involves loss of information, and this loss enables computational gains.

3.3 Summary condition relationships and algorithms

In order to derive summary conditions according to their definitions, we need to be able to recognize achieve, clobber, and undo relationships based on summary conditions as we did for basic CHiP conditions. We give definitions and algorithms for these, which build on constructs and algorithms for reasoning about temporal relationships, described in Appendix A.

Achieving and clobbering are very similar, so we define them together. Definition 11 states that plan $p_1$ must [achieve, clobber] summary precondition $c_2$ of $p_2$ if and only if for all executions of any two plans, $p_1'$ and $p_2'$, with the same summary information and ordering constraints as $p_1$ and $p_2$, the execution of $p_1'$ or one of its subexecutions would [achieve, clobber] an external precondition $\ell(c_2)$ of $p_2'$.

Definition 11   $$\begin{array}{@{}l@{}l@{}l} must&\_[achieve,clobber] \_preco... ...ndition(\ell(c_2),e_{p_2'}) \end{array} \end{array}\end{array}$$

Achieving and clobbering in- and postconditions are defined the same as Definition 11 but substituting ``in'' and ``post'' for ``pre'' and removing the last line for inconditions. Additionally substituting $\exists$ for $\forall$ gives the definitions of may achieve and clobber. Furthermore, the definitions of must/may-undo are obtained by substituting ``post'' for ``pre'' and ``undo'' for ``achieve'' in Definition 11. Note that, as mentioned in Section 2.5, achieving inconditions and postconditions does not make sense for this formalism.

Algorithms for these interactions are given in Figure 6 and Figure 7. These algorithms build on others (detailed in Appendix B) that use interval point algebra to determine whether a plan must or may assert a summary condition before, at, or during the time another plan requires a summary condition to hold. Similar to Definition 3 of must-achieve for CHiP conditions, Figure 6 says that $p'$ achieves summary condition $c$ if it must asserts the condition before it must hold, and there are no other plans that may assert the condition or its negative in between. The algorithm for may-achieve (in Figure 7) mainly differs in that $p'$ may assert the condition beforehand, and there is no plan that must assert in between. The undo algorithms are the same as those for achieve after swapping $c$ and $c'$ in all $must$/$may$-$assert$ lines.

Figure 6: Algorithm for whether a plan must achieve or clobber a summary condition

Figure 7: Algorithm for whether a plan may achieve or clobber a summary condition

The complexity of determining must/may-clobber for inconditions and postconditions is simply $O(c)$ to check $c$ conditions in $p'$. If the conditions are hashed, then the algorithm is constant time. For the rest of the algorithm cases, the complexity of walking through the summary conditions checking for $p''$ and $c''$ is $O(nc)$ for a maximum of $c$ summary conditions for each of $n$ plans represented in $P_{sum}$. In the worst case, all summary conditions summarize the same propositional variable, and all $O(nc)$ conditions must be visited.

Let's look at some examples of these relationships. In Figure 8a, $p' = equip\_M2\_tool$ may-clobber $c$ = $available$(M2)MaS in the summary preconditions of $p = produce\_G$ because there is some history where $equip\_M2\_tool$ ends before $produce\_G$ starts, and $calibrate\_M2$ starts after $produce\_G$ starts. In Figure 8b, $p' = build\_H$ must-achieve $c$ = $available$(H)MuF in the summary preconditions of $p = move\_H$. Here, $c'$ is $available$(H)MuL in the summary postconditions of $build\_H$. In all histories, $build\_H$ attempts to assert $c'$ before the $move\_H$ requires $c$ to be met, and there is no other plan execution that attempts to assert a condition on the availability of H. $equip\_M2\_tool$ does not may-clobber $c$ = $available$(M2)MuF in the summary preconditions of $build\_H$ even though $equip\_M2\_tool$ asserts $c'$ = $\neg available$(M2)MuL before $c$ is required to be met. This is because $calibrate\_M2$ must assert $\neg available$(M2)MuA between the time that $equip\_M2\_tool$ asserts $c'$ and when $c$ is required. Thus, $calibrate\_M2$ must-undo $equip\_M2\_tool$ 's summary postcondition. Because $calibrate\_M2$ cannot assert its postcondition $available$(M2)MuL before $build\_H$ requires $available$(M2)MuF, $calibrate\_M2$ must-clobber the summary precondition.

Figure 8: The production and facilities managers' plans partially expanded. a) The managers' plans unordered with respect to each other. b) $equip\_M2\_tool$ must clobber $available$(M2)MaL of $produce\_G$, and $calibrate\_M2$ must clobber $available$(M2)MuF of $build\_H$.

3.4 Deriving Summary Conditions

Now that we have algorithms that determine interactions of abstract plans based on their summary conditions, we can create an algorithm that derives summary conditions according to their definitions in Section 3.2. Figure 9 shows pseudocode for the algorithm. The method for deriving the summary conditions of a plan $p$ is recursive. First, summary information is derived for each of $p$'s subplans. Then conditions are added based on $p$'s own conditions. Most of the rest of the algorithm derives summary conditions from those of $p$'s subplans. Whether $p$ is $consistent$ depends on the consistency of its subplans and whether its own summary conditions and resource usages are in conflict. The braces '{' '}' used here have slightly different semantics than used before with the brackets. An expression {$x$,$y$} can be interpreted simply as ($x$ or $y$, respectively).

Figure 9: Algorithm for deriving summary information

Definitions and algorithms for temporal relationships such as $always$-$first$ and covers are in Appendix A. When the algorithm adds or copies a condition to a set, only one condition can exist for any literal, so a condition's information may be overwritten if it has the same literal. In all cases, $must$ overwrites $may$; and $first$, $last$, and $always$ overwrite $sometimes$; but, not vice-versa. Further, because it uses recursion, this procedure is assumed to work on plans whose expansion is finite.

3.5 Summary Resource Usage

In this section, we define a representation for capturing ranges of usage both local to the task interval and the depleted usage lasting after the end of the interval. Based on this we introduce a summarization algorithm that captures in these ranges the uncertainty represented by decomposition choices in $or$ plans and partial temporal orderings of $and$ plan subtasks. This representation allows a coordinator or planner to reason about the potential for conflicts for a set of tasks. We will discuss this reasoning later in Section 4.2. Although referred to as resources, these variables could be durations or additive costs or rewards.

3.5.1 Representation

We start with a new example for simplicity that motivates our choice of representation. Consider the task of coordinating a collection of rovers as they explore the environment around a lander on Mars. This exploration takes the form of visiting different locations and making observations. Each traversal between locations follows established paths to minimize effort and risk. These paths combine to form a network like the one mapped out in Figure 10, where vertices denote distinguished locations, and edges denote allowed paths. Thinner edges are harder to traverse, and labeled points have associated observation goals. While some paths are over hard ground, others are over loose sand where traversal is harder since a rover can slip.

Figure 10: Example map of established paths between points in a rover domain

Figure 11 gives an example of an abstract task. Imagine a rover that wants to make an early morning trip from point $A$ to point $B$ on the example map. During this trip the sun slowly rises above the horizon giving the rover the ability to progressively use soak rays tasks to provide more solar power (a non-consumable resource³) to motors in the wheels. In addition to collecting photons, the morning traverse moves the rover, and the resultant go tasks require path dependent amounts of power. While a rover traveling from point $A$ to point $B$ can take any number of paths, the shortest three involve following one, two, or three steps.

Figure 11: $and$/$or$ tree defining a rover's tasks and their resource usages

A summarized resource usage consists of ranges of potential resource usage amounts during and after performing an abstract task, and we represent this summary information for a plan $p$ on a resource $res$ using the structure $$usage_{sum}(p, res) = \langle local\_min(p,res),local\_max(p,res),persist(p,res)\rangle,$$ where the resource's local usage occurs within $p$'s execution, and the persistent usage represents the usage that lasts after the execution terminates for consumable resources.

Definition 12   $$\setlength{\arraycolsep}{0in} \begin{array}[t]{lll} usage_{... ...p\in E(h)}(-r(res,h,t_f(e_p)))]& \rangle \end{array}\end{array}$$

The context for Definition 12 is the set of all histories $H$ where the value of $res$ is 0 in the initial state, and $E(h)$ only contains the execution of $p$ and its subexecutions. Thus, the $-r(res,h,t)$ term is the combined usage of $res$ at time $t$ of all executions in the hierarchy as defined in Section 2.4. So, the maximum of the $local\_min$ is the highest among all histories of the lowest point of usage during $p$'s execution. The usage ranges capture the multiple possible usage profiles of a task with multiple decomposition choices and timing choices among loosely constrained subtasks. For example, the high path task has a $\langle$[4,4],[6,6],[0,0]$\rangle$ summary power use over a 40 minute interval. In this case the ranges are single points due to no uncertainty - the task simply uses 4 watts for 15 minutes followed by 6 watts for 25 minutes. The $move$(A,B) task provides a slightly more complex example due to its decompositional uncertainty. This task has a $\langle$[0,4],[4,6],[0,0]$\rangle$ summary power use over a 50 minute interval. In both cases the $persist$ is [0,0] because solar power is a non-consumable resource.

As an example of reasoning with resource usage summaries, suppose that only 3 watts of power were available during a $move$(A,B) task. Given the [4,6] $local\_max$, we know that there is not enough power no matter how the task is decomposed. Raising the available power to 4 watts makes the task executable depending on how it gets decomposed and scheduled, and raising to 6 or more watts makes the task executable for all possible decompositions.

This representation of abstract (or uncertain) metric resource usage can be seen as an extension of tracking optimistic and pessimistic resource levels [Drabble Tate, 1994]. Computing only the upper and lower bounds on resource usage for an abstract plan gives some information about whether lower or upper bound constraints on a resource may, must, or must not be violated, but it is not complete. By representing upper and lower bounds as ranges of these bounds over all potential histories, we can certainly know whether bounds may, must, or must not be violated over all histories. For the example above, if we only tracked one range for the local usage, [0,6], we would not know that there is definitely a conflict when only 3 watts are available. Knowing this extra information can avoid exploration of an infeasible search space.

3.5.2 Resource Summarization Algorithm

The state summarization algorithm in Section 3.4 recursively propagates summary conditions upwards from an $and$/$or$ hierarchy's leaves, and the algorithm for resource summarization takes the same approach. Starting at the leaves, the algorithm finds primitive tasks that use constant amounts of a resource. The resource summary of a task using $x$ units of a resource is $\langle[x$,$x]$,$[x$,$x]$,$[0$,$0]\rangle$ or $\langle[x$,$x]$,$[x$,$x]$,$[x$,$x]\rangle$ over the task's duration for non-consumable or consumable resources respectively.

Moving up the $and$/$or$ tree, the summarization algorithm either comes to an $and$ or an $or$ branch. For an $or$ branch the combined summary usage comes from the $or$ computation $$\setlength{\arraycolsep}{0in} \begin{array}[t]{lllll} \lang... ... & max_{c \in children}(ub(persist(c)))]&\ \rangle, \end{array}$$ where $lb()$ and $ub()$ extract the lower bound and upper bound of a range respectively. The $children$ denote the branch's children with their durations extended to the length of the longest child. This duration extension alters a child's resource summary information because the child's usage profile has a zero resource usage during the extension. For instance, in determining the resource usage for $move$(A,B), the algorithm combines two 40 minute tasks with a 50 minute task. The resulting summary information describes a 50 minute abstract task whose profile might have a zero watt power usage for 10 minutes. This extension is why $move$(A,B) has a [0,4] for a $local\_min$ instead of [3,4]. Planners that reason about variable durations could use [3,4] for a duration ranging from 40 to 50.

Computing an $and$ branch's summary information is a bit more complicated due to timing choices among loosely constrained subtasks. The take $x$ path examples illustrate the simplest sub-case, where subtasks are tightly constrained to execute serially. Here profiles are appended together, and the resulting summary usage information comes from the SERIAL-AND computation $$\setlength{\arraycolsep}{0in} \begin{array}[t]{lllll} \lang... ...a_{c \in children}(ub(persist(c)))] & \ \rangle,\\ \end{array}$$ where $\Sigma_{lb}^{pre}(c)$ and $\Sigma_{ub}^{pre}(c)$ are the respective lower and upper bounds on the cumulative persistent usages of children that execute before $c$. These computations have the same form as the $\Sigma$ computations for the final $persist$.

The case where all subtasks execute in parallel and have identical durations is slightly simpler. Here the usage profiles add together, and the branch's resultant summary usage comes from the PARALLEL-AND computation $$\setlength{\arraycolsep}{0in} \begin{array}[t]{lllll} \lang... ...a_{c \in children}(ub(persist(c)))] & \ \rangle,\\ \end{array}$$ where $\Sigma_{ub}^{non}(c)$ and $\Sigma_{lb}^{non}(c)$ are the respective sums of the $local\_max$ upper bounds and the $local\_min$ lower bounds for all children except $c$.

To handle $and$ tasks with loose temporal constraints, we consider all legal orderings of child task endpoints. For example, in the rover's early morning tasks, there are three serial solar energy collection subtasks running in parallel with a subtask to drive to location $B$. Figure 12 shows one possible ordering of the subtask endpoints, which breaks $move$(A,B) into three pieces, and two of the soak rays children in half. Given an ordering, the summarization algorithm can (1) use the endpoints of the children to determine subintervals, (2) compute summary information for each child task/subinterval combination, (3) combine the parallel subinterval summaries using the PARALLEL-AND computation, and then (4) chain the subintervals together using the SERIAL-AND computation. Finally, the $and$ task's summary is computed by combining the summaries for all possible orderings using an $or$ computation.

Figure 12: Possible task ordering for a rover's morning activities, with resulting subintervals.

Here we describe how step (2) generates different summary resource usages for the subintervals of a child task. A child task with summary resource usage $\langle[a$,$b]$,$[c$,$d]$,$[e$,$f]\rangle$ contributes one of two summary resource usages to each intersecting subinterval⁴: $$\langle[a,b],[c,d],[0,0]\rangle,\langle[a,d],[a,d],[0,0]\rangle.$$ While the first usage has the tighter [$a$,$b$],[$c$,$d$] local ranges, the second has looser [$a$,$d$],[$a$,$d$] local ranges. Since the $b$ and $c$ bounds only apply to the subintervals containing the subtask's minimum and maximum usages, the tighter ranges apply to one of a subtask's intersecting subintervals. While the minimum and maximum usages may not occur in the same subinterval, symmetry arguments let us connect them in the computation. Thus one subinterval has tighter local ranges and all other intersecting subintervals get the looser local ranges, and the extra complexity comes from having to investigate all subtask/subinterval assignment options. For instance, there are three subintervals intersecting $move$(A,B) in Figure 12, and three different assignments of summary resource usages to the subintervals: placing [0,4],[4,6] in one subinterval with [0,6],[0,6] in the other two. These placement options result in a subtask with $n$ subintervals having $n$ possible subinterval assignments. So if there are $m$ child tasks each with $n$ alternate assignments, then there are $n^{m}$ combinations of potential subtask/subinterval summary resource usage assignments. Thus propagating summary information through an $and$ branch is exponential in the number of subtasks with multiple internal subintervals. However since the number of subtasks is controlled by the domain modeler and is usually bounded by a constant, this computation is tractable. In addition, summary information can often be derived offline for a domain. The propagation algorithm takes on the form:

• For each consistent ordering of endpoints:
  • For each consistent subtask/subinterval summary usage assignment:
    • Use PARALLEL-AND computations to combine subtask/subinterval summary usages by subinterval.
    • Use a SERIAL-AND computation on the subintervals' combined summary usages to get a consistent summary usage.
• Use $or$ computation to combine all consistent summary usages to get $and$ task's summary usage.

Now that we have described how to derive summary information, we can discuss how to use it.

4 Identifying Abstract Solutions

Up to this point, we have detailed algorithms for deriving summary conditions and for reasoning about potential ($may$) and definite ($must$) interactions between tasks based on their summary information. In addition, we have outlined algorithms for deriving summarized resource usage but have not yet discussed how to identify solutions at abstract levels. In this section, we show how the interactions of summary conditions and summarized metric resource usages identify potentially resolvable threats and unresolvable conflicts among the plans of a group of agents.

4.1 Threats on Summary Conditions

Agents can attempt to resolve conflicts among their plans by considering commitments to particular decompositions and ordering constraints. In order to do this, the agents must be able to identify remaining conflicts (threats) among their plans. Here we present simple algorithms for reasoning about threats between abstract plans and their required conditions.

Formally, for a set of CHiPs $P$ with ordering constraints $order$, a threat between an abstract plan $p\in P$ and a summary condition $c'$ of another plan $p'\in P$ exists iff $p$ may-clobber $c'$. We say that the threat is unresolvable if $p$ must-clobber $c'$ and $must(c')$ because there are no decomposition choices or ordering constraints that could be added to resolve the threat.

So, a simple algorithm for identifying threats is to check to see if each of the $O(nc)$ summary conditions of $n$ plans in $P_{sum}$ is must- or may-clobbered by any other plan. Since the complexity of checking to see if a particular condition is must- or may-clobbered is $O(nc)$, this algorithm's complexity is $O(n^2c^2)$.

In many coordination tasks, if agents could determine that under certain temporal constraints their plans can be decomposed in any way ($CanAnyWay$) or that under those constraints there is no way they can be successfully decomposed ($\neg MightSomeWay$), then they can make coordination decisions at abstract levels without entering a potentially costly search for valid plan merges at lower levels. Here are the formal definitions of $CanAnyWay$ and $MightSomeWay$:

Definition 13   $$\begin{array}{@{}l@{}l} [CanAnyWay&,MightSomeWay](order, P_{... ... \\ &[\forall, \exists] e \in E(h), succeeds(e,h) \end{array}$$

Definition 13 states that the plans with summary information $P_{sum}$ under ordering constraints can execute in any way if and only if all sets of plans $P$ that have summary information $P_{sum}$ will execute successfully in any history. $MightSomeWay$ is true if there is some set of plans that could possibly execute successfully. We could also describe $CanSomeWay(order$,$P_{sum})$ and $MightAnyWay(rel$,$P_{sum})$ in the same fashion, but it is not obvious how their addition could further influence search. Exploring these relations may be an interesting topic for future research.

In Figure 13a, the three top-level plans of the managers are unordered with respect to each other. The leaf plans of the partially expanded hierarchies comprise $P_{sum}$. Arrows represent the constraints in $order$. $CanAnyWay$({},{$produce\_G$, $maintenance$, $move\_parts$}) is false because there are several conflicts over the use of machines and transports that could occur for certain executions of the plans as described in Section 3.3 for Figure 8. However, $MightSomeWay$({}, {$produce\_G$, $maintenance$, $move\_parts$}) is true because the plans might in some way execute successfully as shown in Figure 13b. With the ordering constraints in Figure 13b, $CanAnyWay$({before(1,0), before(0,2)},{$produce\_G$, $maintenance$, $move\_parts$}) is true because the plans can execute in any way consistent with these ordering constraints without conflict. Figure 8b is an example where $MightSomeWay$ is false because $calibrate\_M2$ must-clobber the $available$(M2)MuF summary precondition of $build\_H$.

Figure 13: The top-level plans of each of the managers for the manufacturing domain

Figure 14: Algorithm determining whether plans with the given summary information CanAnyWay or MightSomeWay execute successfully.

As shown in Figure 14, the algorithm for determining $CanAnyWay$ for summary conditions is simple in that it only needs to check for threats. $MightSomeWay$ is more complicated because just checking for an unresolvable threat is not enough. As shown in Figure 15, it is not the case that plan $p$ must clobber $p'$ because $p''$ could come between and achieve the precondition $\ell$ of $p'$. Thus, $p$ may-clobbers $\ell$ in $p$ and in $p''$. However, obviously $p$ will clobber one or the other, so $MightSomeWay$ is false. In order to determine $MightSomeWay$ is $false$, an agent must exhaustively search through an exponential number of schedules to see if not all conflicts can be resolved. Instead of performing an exponential search to determine $MightSomeWay$, we use the simple algorithm in Figure 14 that just checks for must-clobber relationships. In Section 5.1 we describe a more flexible search to find conflict-free abstract plans than just scheduling at an abstract level.

Figure 15: $MightSomeWay$ is false even though there is no must-clobber relationship.

Thus, while the $CanAnyWay$ algorithm is sound and complete, the $MightSomeWay$ algorithm is complete but not sound. This also means that determining $\neg MightSomeWay$ is sound but not complete. We will still make use of both of these algorithms in a sound and complete planning/coordination algorithm in Section 5.1. The complexity of these algorithms is $O(n^2c^2)$ since the $O(nc)$ procedures for determining must/may-clobber must be run for each of $nc$ conditions ($c$ summary conditions in each of $n$ plans represented by $P_{sum}$).

4.2 Summary Resource Usage Threats

Planners detect threats on resource constraints in different ways. If the planner reasons about partially ordered actions, it must consider which combinations of actions can overlap and together exceed (or fall below) the resource's maximum value (or minimum value). A polynomial algorithm does this for the IxTeT planner [Laborie Ghallab, 1995]. Other planners that consider total order plans can more simply project the levels of the resource from the initial state through the plan, summing overlapping usages, to see if there are conflicts []<e.g.,>rabideau:00.

Finding conflicts involving summarized resource usages can work in the same way. For the partial order planner, the resultant usage of clusters of actions are tested using the PARALLEL-AND algorithm in Section 3.5. For the total order planner, the level of the resource is represented as a summarized usage, initially $\langle$[$x$, $x$], [$x$, $x$], [$x$, $x$]$\rangle$ for a consumable resource with an initial level $x$ and $\langle$[$x$, $x$], [$x$, $x$], [0, 0]$\rangle$ for a non-consumable resource. Then, for each subinterval between start and end times of the schedule of tasks, the summary usage for each is computed using the PARALLEL-AND algorithm. Then the level of the resource is computed for each subinterval while propagating persistent usages using the SERIAL-AND algorithm.

We can decide $CanAnyWay$ and $MightSomeWay$ as defined in Section 4.1, in terms of the summary usage values resulting from invocations of PARALLEL-AND and SERIAL-AND in the propagation algorithm at the end of Section 3.5.2. $CanAnyWay(order, P_{sum}, res)$ is true if and only if there are no potential threats. These algorithms discover a threat if they ever compute an interval $i$ such that

$$\setlength{\arraycolsep}{0in} \begin{array}[t]{lllll} lb(lo... ...alue(res)\ \vee \ ub(persist(i)) > max\_value(res). \end{array}$$

$MightSomeWay(order, P_{sum}, res)$ is true if and only if there is a possible run with potentially no threats. SERIAL-AND discovers such a run if it returns a summary usage where

$$\setlength{\arraycolsep}{0in} \begin{array}[t]{lllll} ub(lo... ...res)\ \wedge \ ub(persist(i)) \leq max\_value(res). \end{array}$$

Now that we have mechanisms for deriving summary information and evaluating plans based on their summarizations, we will discuss how to exploit them in a planning/coordination algorithm.

5 Hierarchical Planning and Coordination Algorithm

With the earlier defined algorithms for reasoning about a group of agents' plans at multiple levels of abstraction, we now describe how agents can efficiently plan and coordinate based on summary information. We describe a coordination algorithm that searches for ways to restrict the decomposition and ordering of the collective actions of the agent(s) in order to resolve conflicts while maximizing the utilities of the individual agents or the global utility of the group.

Our approach starts by making planning decisions at the most abstract level and, as needed, decomposes the agents' plans in a top-down fashion. The idea is to introduce only the information that is needed. Introducing irrelevant details complicates search and increases communication. After describing the top-down planning/coordination algorithm, we describe search techniques and heuristics that the algorithm can use to further exploit summary information.

5.1 Top-Down Hierarchical Planning and Coordination

The formalism of summary conditions culminated in Section 4 in algorithms that determine if a set of plans (abstract or primitive) under a partial set of ordering constraints is definitely conflict-free ($CanAnyWay$) or has unresolvable conflicts ($\neg MightSomeWay$). Here we integrate these algorithms into one that searches for a consistent plan for one or more agents. The particular algorithm we describe here is shown to be sound and complete [Clement, 2002]. The search starts out with the top-level plans of each agent. A solution is one where there are no possible conflicts among the agents' plans. The algorithm tries to find a solution at this top level and then expands the hierarchies deeper and deeper until the optimal solution is found or the search space has been exhausted. A pseudocode description of the algorithm is given in Figure 16.

A state of the search is a partially elaborated plan that we represent as a set of $and$ plans (one for each agent), a set of temporal constraints, and a set of blocked plans. The subplans of the $and$ plans are the leaves of the partially expanded hierarchies of the agents. The set of temporal constraints includes synchronization constraints added during the search in addition to those dictated by the agents' individual hierarchical plans. Blocked subplans keep track of pruned $or$ subplans.

Decisions can be made during search in a decentralized fashion. The agents can negotiate over ordering constraints to adopt, over choices of subplans to accomplish higher level plans, and over which decompositions to explore first. While the algorithm described here does not specify (or commit to) any negotiation technique, it does provide the mechanisms for identifying the choices over which the agents can negotiate. Although agents can make search decisions in a decentralized fashion, we describe the algorithm given here as a centralized process that requests summary information from the agents being coordinated.

In the pseudocode in Figure 16, the coordinating agent collects summary information about the other agents' plans as it decomposes them. The $queue$ keeps track of expanded search states. If the $CanAnyWay$ relation holds for the search state, the Dominates function determines if the current solutions are better for every agent than the solution represented by the current search state and keeps it if the solution is not dominated. If $MightSomeWay$ is false, then the search space rooted at the current search state can be pruned; otherwise, the coordinator applies operators to generate new search states.

The operators for generating successor search states are expanding non-primitive plans, blocking $or$ subplans, and adding temporal constraints on pairs of plans. When an agent expands one of its plans, each of the plan's summary conditions are replaced with only the original conditions of the parent plan. Then the subplans' summary information and ordering constraints are added to the search state. A subplan of an $or$ plan is added (or selected) only when all other subplans are blocked. When ApplyOperator is called for the select and block operators, search states are generated for each selectable and blockable subplan, respectively. Blocking an $or$ subplan can be effective in resolving a constraint in which the other $or$ subplans are not involved. For example, if the inventory manager plans to only use transport2, the production manager could block subplans using transport2, leaving subplans using transport1 that do not conflict with the inventory manager's plan. This can lead to least commitment abstract solutions that leave the agents flexibility in selecting among the multiple applicable remaining subplans. The agents can take another approach by selecting a subplan (effectively blocking all of the others) to investigate a preferred choice or one that more likely avoids conflicts.

When the operator is to add a temporal constraint, a new search state is created for each alternative temporal constraint that could be added. These successor states are enqueued so that if backtracking is needed, each alternative can be tried. Adding temporal constraints should only generate new search states when the ordering is consistent with the other global and local constraints. In our implementation, we only add constraints that will help resolve threats as determined by the must/may achieves and clobbers algorithms. When a plan is expanded or selected, the ordering constraints must be updated for the subplans that are added.

Figure 16: A concurrent hierarchical coordination algorithm.

The soundness and completeness of the coordination algorithm depends on the soundness and completeness of identifying solutions and the complete exploration of the search space. Soundness and completeness is not defined with respect to achieving particular goal predicates but resolving conflicts in the plan hierarchies. A domain modeler may represent goals as abstract CHiPs that decompose into possible plans that accomplish them or as a series of actions for an agent to execute successfully.

Consider how the algorithm would find coordinated plans for the manufacturing agents. At the beginning of the search, a coordinating agent gathers the summary information for the top-level plans of the three agents in $plans$. At first, there are no ordering constraints, so $order$ is empty in the first search state (shown in Figure 13a) popped from the $queue$. $CanAnyWay$ is false, and $MightSomeWay$ is true for this state as described earlier in this section, so the coordinator chooses an $operator$ to apply to the search state. It could choose constrain and order the $maintenance$ plan before $produce\_H$ to resolve all conflicts between those two plans. The $order$ is updated with the new constraint, and the new search state is inserted into the $queue$ by according to some ranking function. On the next iteration of the loop, the only search state in the queue that was just inserted is popped. The coordinator again finds that $CanAnyWay$ is false, and $MightSomeWay$ is true since $move\_parts$ may still conflict with other plans over the use of transports. It can choose to constrain $produce\_H$ before $move\_parts$ to resolve the remaining conflicts. This is detected on the next cycle of the search loop where $CanAnyWay$ is found to be true for this search state (shown in Figure 13b). The $plans$, the two constraints in $order$, and the empty set of blocked plans are added as a solution since there is no previously found solution that Dominates it. The Dominates function uses domain specific criteria for determining when a solution has value as an alternative and should be kept or is inferior compared to another and should be dropped. In this manufacturing domain, one solution dominates another if the finish time for at least one agent is earlier and no finish times are later for any agents. The search then continues to find alternative or superior solutions, although the agents may decide to terminate the search in the interest of time.

5.2 Search Techniques and Heuristics

Although summary information is valuable for finding conflict free or coordinated plans at abstract levels, this information can also be valuable in directing the search to avoid branches in the search space that lead to inconsistent or suboptimal coordinated plans. A coordinator can prune away inconsistent coordinated plans at the abstract level by doing a quick check to see if $MightSomeWay$ is false. For example, if the search somehow reached the state shown in Figure 8b, the coordinator could backtrack before expanding the hierarchies further and avoid reasoning about details of the plans where they must fail.

Another strategy is to first expand plans involved in the most threats. For the sake of completeness, the order of plan expansions does not matter as long as they are all expanded at some point when the search trail cannot be pruned. But, employing this ``expand on most threats first'' (EMTF) heuristic aims at driving the search down through the hierarchy to find the subplan(s) causing conflicts with others so that they can be resolved more quickly. This is similar to a most-constrained variable heuristic often employed in constraint satisfaction problems. For example, if the facilities and inventory managers wished to execute their plans concurrently as shown in Figure 17a, at the most abstract level, the coordinator would find that there are conflicts over the use of transports for moving parts. Instead of decomposing $produce\_H$ and reasoning about plan details where there are no conflicts, the EMTF heuristic would choose to decompose either $maintenance$ or $move\_parts$ which have the most conflicts. By decomposing $maintenance$ the agents can resolve the remaining conflicts and still execute concurrently.

Figure 17: EMTF heuristic resolving conflicts by decomposing the $maintenance$ plan

Another heuristic that a coordinator can use in parallel with EMTF is ``choose fewest threats first'' (CFTF). Here the search orders states in the search queue by ascending numbers of threats left to resolve. In effect, this is a least-constraining value heuristic used in constraint satisfaction approaches. As mentioned in Section 4.1, threats are identified by the $CanAnyWay$ algorithm. By trying to resolve the threats of coordinated plan search states with fewer conflicts, it is hoped that solutions can be found more quickly. So, EMTF is a heuristic for ordering $and$ subplans to expand, and CFTF, in effect, orders $or$ subplan choices. For example, if the production manager chooses to use machine M1 instead of M2 to produce G, the coordinator is likely closer to a solution because there are fewer conflicts to resolve. This heuristic can be applied not only to selecting $or$ subplan choices but also to choosing temporal constraints and variable bindings or any search operator from the entire set of operators.

In addition, in trying to find optimal solutions in the style of a branch-and-bound search, the coordinator can use the cost of abstract solutions to prune away branches of the search space whose minimum cost is greater than the maximum cost of the current best solution. This is the role of the Dominates function in the description of the coordination algorithm in Section 5.1. This usually assumes that cost/utility information is decomposable over the hierarchy of actions, or the cost of any abstract action is a function of its decompositions.

6 Complexity Analyses

Even though the planner or coordinator can use the search techniques described in the Section 5.2 to prune the search space, just being able to find solutions at multiple levels of abstraction can reduce the computation as much as doubly exponentially. In this section, we give an example of this and then analyze the complexity of planning and scheduling to characterize this cost reduction and the conditions under which it occurs.

An agent that interleaves execution with planning/coordination often must limit the total computation and execution cost required to achieve its goals. The planning algorithm described in Section 5.1 is able to search for solutions at different levels of abstraction. For the manufacturing example, our implementation of a centralized coordinator uses this algorithm to find in 1.9 CPU seconds a solution at the top level of the agents' plans as shown in Figure 13b. If we define the cost of execution as the makespan (completion time) of the coordinated plan, the cost of this solution is 210 where the makespan of the production manager's plan is 90, the facilities manager's is 90, and the inventory manager's is 30. For the solution in Figure 13c, the coordinator required 667 CPU seconds, and the makespan of the coordinated plan is 170. Another solution is found at an intermediate level of abstraction, taking 69 CPU seconds and having a makespan of 180. So, with a little more effort, the algorithm expanded the hierarchy to an intermediate level where the cost of the solution was reduced by 30. Thus, overall cost can be reduced by coordinating at intermediate levels.

For this problem, coordinating at higher levels of abstraction is less costly because there are fewer plan steps. But, even though there are fewer plans at higher levels, those plans may have greater numbers of summary conditions to reason about because they are collected from the much greater set of plans below. Here we argue that even in the worst case where the number of summary conditions per plan increases exponentially up the hierarchy, finding solutions at abstract levels is expected to be exponentially cheaper than at lower levels. We first analyze the complexity of the summarization algorithm to help the reader understand how the summary conditions can collect in greater sets at higher levels.

6.1 Complexity of Summarization

Consider a hierarchy with $n$ total plans, $b$ subplans for each non-primitive plan, and depth $d$, starting with zero at the root, as shown in Figure 18. The procedure for deriving summary conditions works by basically propagating the conditions from the primitives up the hierarchy to the most abstract plans. Because the conditions of any non-primitive plan depend only on those of its immediate subplans, deriving summary conditions can be done quickly if the number of subplans is not large. The derivation algorithm mainly involves checking for achieve, clobber, and undo interactions among subplans for all possible total orderings of the subplans (as described in Section 3.4). Checking for one of these relations for one summary condition of one subplan is $O(bs)$ for $b$ subplans, each with $s$ summary conditions (as discussed in Section 3.3). Since there are $O(bs)$ conditions that must be checked in the set of subplans, deriving the summary conditions of one plan from its subplans is $O(b^2s^2)$.

However, the maximum number of summary conditions for a subplan grows exponentially up the hierarchy since, in the worst case, no summary conditions merge during summarization. This happens when the conditions of each subplan are on completely different propositions/variables than those of any sibling subplan. In this case, a separate summary condition will be generated for each summary condition of each subplan. If the children share conditions on the same variable, this information is collapsed into a single summary condition in the parent plan.

As shown in the third column of the table in Figure 18, a plan at the lowest level $d$ has $s=c$ summary conditions derived from its $c$ pre-, in-, and postconditions. A plan at level $d-1$ derives $c$ summary conditions from its own conditions and $c$ from each of its $b$ subplans giving $c+bc$ summary conditions, or $s=O(bc)$. So, in this worst case $s=O(b^{d-i}c)$ for a plan at level $i$ in a hierarchy for which each plan has $c$ (non-summary) conditions. Thus, the complexity of summarizing a plan at level $i$ (with subplans at level $i+1$) is $O(b^2b^{2(d-(i+1))}c^2)=O(b^{2(d-i)}c^2)$. There are $b^i$ plans at level $i$ (second column in the figure), so the complexity of summarizing the set of plans at level $i$ is $O(b^ib^{2(d-i)}c^2)=O(b^{2d-i}c^2)$ as shown in the fourth column in the figure. Thus, the complexity of summarizing the entire hierarchy of plans would be $O(\sum_{i=0}^{d-1} b^i b^{2(d-i)}c^2)$. In this summation $i=0$ dominates, so the complexity can be simplified to $O(b^{2d}c^2)$. If there are $n=O(b^d)$ plans in the hierarchy, we can write this simply as $O(n^2c^2)$, which is the square of the size of the hierarchy.

In the best case where all conditions are on the same variable, each plan will have $c$ summary conditions. Thus, the complexity for summarizing the hierarchy will be $O(\sum_{i=0}^{d-1} b^i b^2c^2)$, which simplifies to $O(b^{d+1}c^2) = O(nbc^2)$. In any case, the summarization of conditions is tractable, and as we discussed in Section 3.5.2, the summarization of resources is also tractable.

6.2 Complexity of Finding Abstract Solutions

In order to resolve conflicts (and potentially arrive at a solution) at a particular level of expansion of the hierarchy, the coordination algorithm checks for threats between the plans under particular ordering constraints at that level. Checking for threats involves finding clobber relations among the plans and their summary conditions. The complexity of finding threats among $n$ plans each with $s$ summary conditions is $O(n^2s^2)$ as shown in Section 4.1 for the $MightSomeWay$ algorithm. For a hierarchy expanded to level $i$, there are $n=O(b^i)$ plans at the frontier of expansion, and each plan has $s=O(b^{d-i}c)$ summary conditions. So, as shown in the fifth column of the table in Figure 18, the worst case complexity of checking for threats for one synchronization of a set of plans at level $i$ is $O(b^{2i}(b^{d-i}c)^2)=O(b^{2d}c^2)$. Notice that $i$ drops out of the formula, meaning that the complexity of checking a candidate solution is independent of the depth level. In the best case where summary conditions fully merge, each plan has $s=c$ summary conditions, so the complexity of checking a candidate solution is $O(b^{2i}c^2)$, a factor of $O(b^{2(d-i)})$faster than the worst case.

Figure 18: Complexity of threat identification and resolution at abstract levels

However, the algorithm may check many synchronizations at a particular level before finding a solution or exhausting the search space. In fact this search complexity grows exponentially with the number of plans.⁵ Thus, as shown in the last column of the table in Figure 18, the search space is $O(k^{b^i})$ for $b^i$ plans at level $i$ and constant $k$.⁶ Thus, the search space grows doubly exponentially down the hierarchy based on the number of plan steps.

In our refinement coordination and planning algorithm, the conflict detection is a basic operation that is done for resolving conflicts. So, to also include the effect of the size of conditions (in addition to plan steps) on the complexity of the planning/coordination algorithm, we must multiply by the complexity to check threats. Thus, the complexity is $O(k^{b^i} b^{2d}c^2)$ when summary information does not merge at all and $O(k^{b^i} b^{2i}c^2)$ when summary information fully merges. The complexity of resolving conflicts at the primitive level is $O(k^{b^d} b^{2d}c^2)$, so resolving conflicts at an abstract level speeds search doubly exponentially, a factor of $O(k^{b^d-b^i})$ even when summary information does not merge during summarization. Now, if it completely merges, the speedup is a factor of $O(k^{b^d-b^i} b^{2(d-i)})$.

There are only $and$ plans in this analysis. In the case that there are $or$ plans, being able to prune branches at higher levels based on summary information will also greatly improve the search despite the overhead of deriving and using summary conditions. Pruning effectively reduces the branching factor since the branch is eliminated before investigating its details. Thus, the complexity based on the number of plan steps becomes $O(k^{(b-p)^d})$ when a fraction of $p/b$ branches can be pruned. Thus, pruning can also create an exponential reduction in search.

6.3 Scheduling Complexity

A local search planner (e.g. ASPEN, rabideau:00) does not backtrack, but the problem to be solved is the same, so one might expect that complexity advantages are the same as for the refinement planner. However, the search operations for the local search planner can be very different. A previous study of a technique called aggregation eliminates search inefficiencies at lower levels of detail in task hierarchies by operating on hierarchies as single tasks [Knight, Rabideau, Chien, 2000]. Thus, it is not immediately clear what additional improvements a scheduler could obtained using summary information. We will show that the improvements are significant, but first we must provide more background on aggregation.

Moving tasks is a central scheduling operation in iterative repair planners. A planner can more effectively schedule tasks by moving related groups of tasks to preserve constraints among them. Hierarchical task representations are a common way of representing these groups and their constraints. Aggregation involves moving a fully detailed abstract task hierarchy while preserving the temporal ordering constraints among the subtasks. Moving individual tasks independently of their parent, siblings, and subtasks is shown to be much less efficient [Knight, Rabideau, Chien, 2000]. Valid placements of the task hierarchy in the schedule are computed from the state and resource usage profiles for the hierarchy and for the other tasks in the context of the movement. A hierarchy's profile represents one instantiation of the decomposition and temporal ordering of the most abstract task in the hierarchy.

Figure 19: Schedule of $n$ task hierarchies each with $c$ constraints on $v$ variables

Consider a schedule of $n$ task hierarchies with a maximum branching factor $b$ expanded to a maximum depth of $d$ as shown in Figure 19. Suppose each hierarchy has $c$ constraints on each of $v$ variables (states or metric resources). To move a hierarchy of tasks using aggregation, the scheduler must compute valid intervals for each resource variable affected by the hierarchy.⁷ The scheduler then intersects these intervals to get valid placements for the abstract tasks and their children. The complexity of computing the set of valid intervals for a resource is $O(cC)$ where $c$ is the number of constraints (usages) an abstract task has with its children for the variable, and $C$ is the number of constraints of other tasks in the schedule on the variable [Knight, Rabideau, Chien, 2000]. With $n$ similar task hierarchies in the entire schedule, then $C=(n-1)c$, and the complexity of computing valid intervals is $O(nc^2)$. But this computation is done for each of $v$ resource variables (often constant for a domain), so moving a task will have a complexity of $O(vnc^2)$. The intersection of valid intervals across variables does not increase the complexity. Its complexity is $O(tnr)$ because there can be at most $nr$ valid intervals for each timeline; intersecting intervals for a pair of timelines is linear with the number of intervals; and only $t-1$ pairs of timelines need to be intersected to get the intersection of the set.

The summary information of an abstract task represents all of the constraints of its children, but if the children share constraints over the same resource, this information is collapsed into a single summary resource usage in the abstract task. Therefore, when moving an abstract task, the number of different constraints involved may be far fewer depending on the domain. If the scheduler is trying to place a summarized abstract task among other summarized tasks, the computation of valid placement intervals can be greatly reduced because the $c$ in $O(vnc^2)$ is smaller. We now consider the two extreme cases where constraints can be fully collapsed and where they cannot be collapsed at all.

In the case that all tasks in a hierarchy have constraints on the same variable, the number of constraints in a hierarchy is $O(b^d)$ for a hierarchy of depth $d$ and branching factor (number of child tasks per parent) $b$. In aggregation, where hierarchies are fully detailed first, this means that the complexity of moving a task is $O(vnb^{2d})$ because $c=O(b^d)$. Now consider using aggregation for moving a partially expanded hierarchy where the leaves are summarized abstract tasks. If all hierarchies in the schedule are decomposed to level $i$, there are $O(b^i)$ tasks in a hierarchy, each with one summarized constraint representing those of all of the yet undetailed subtasks beneath it for each constraint variable. So $c=O(b^i)$, and the complexity of moving the task is $O(vnb^{2i})$. Thus, moving an abstract task using summary information can be a factor of $O(b^{2(d-i)})$ times faster than for aggregation. Because the worst case number of conflicts increases with the number of plan steps (just as with the refinement planner), the worst case complexity of resolving conflicts based on the number of plan steps at level $i$ is $O(k^{b^i})$. Thus (as with refinement planning) using summary information can make speedups of $O(k^{b^{d-i}}b^{2(d-i)})$ when summary information fully collapses.

The other extreme is when all of the tasks place constraints on different variables. In this case, $c=1$ because any hierarchy can only have one constraint per variable. Fully detailed hierarchies contain $v=O(b^d)$ different variables, so the complexity of moving a task in this case is $O(nb^d)$. If moving a summarized abstract task where all tasks in the schedule are decomposed to level $i$, $v$ is the same because the abstract task summarizes all constraints for each subtask in the hierarchy beneath it, and each of those constraints are on different variables such that no constraints combine when summarized. Thus, the complexity for moving a partially expanded hierarchy is the same as for a fully expanded one. In this case, the number of conflicts also does not change with the depth of the hierarchy because the conflicts are always between pairs of the $n$ hierarchies. So, for this other extreme case, summary information does not reduce the complexity of scheduling and would only incur unnecessary overhead.

Other complexity analyses have shown that different forms of hierarchical problem solving, if they do not need to backtrack from lower to higher levels because there are no interacting subproblems, can reduce the size of the search space by an exponential factor [Korf, 1987, Knoblock, 1991]. A planner or scheduler using summary information can witness exponential improvements without this assumption. Backtracking across abstraction levels occurs within the planner/coordinator described in Section 5.1 when the current search state is $\neg MightSomeWay$ and another $or$ subplan on the same or higher level can be selected. We demonstrated that the search space grows doubly exponentially down the hierarchy because the number of plans grows exponentially, and resolving conflicts grows exponentially with the number of plans. Thus, as long as the planner or coordinator does not have to fully expand all abstract plans to the primitive level and summary information merges at higher levels, the search complexity is reduced at least by a factor of $k^{b^d-b^i}$ where $i$ is the level where the search completed, and $d$ is the depth of the hierarchy. yang:97 also suggests ways exponential speedups can be obtained when subplans interact based on hierarchy structure. Our speedups are complementary to these because summary information limits the decomposition of task hierarchies and compresses the information manipulated by a planner or scheduler.

7 Experiments

Now we experimentally evaluate the use of summary information in planning and coordination for three different domains: an evacuation domain, the manufacturing domain described in Section 1.1, and a multi-rover domain. In these domains, we define performance in different ways to show a range of benefits that abstract reasoning offers.

We evaluate the algorithm described in Section 5.1. Our implementation orders search states in the queue such that those generated by synchronization operators precede those generated by expansion and selection operators. Thus, before going deeper into a part of the hierarchy, the implementation of the algorithm explores all orderings of the agents' plans before digging deeper into the hierarchy. Investigating heuristics for choosing between synchronization and decomposition operators is a topic for future research.

In the next section we report experiments for an evacuation domain that show how abstract reasoning using summary information can find optimal coordination solutions more quickly than conventional search strategies. Optimal solutions in the evacuation domain have minimal global execution times because evacuees must be transported to safety as quickly as possible. In Section 7.2, we show that summary information improves local search performance significantly when tasks within the same hierarchy have constraints over the same resource, and when solutions are found at some level of abstraction. We also evaluate the benefits of using the CFTF and EMTF heuristics for iterative repair and show where summary information can slow search.

In some domains, computation time may be insignificant to communication costs. These costs could be in terms of privacy for self-interested agents, security for sensitive information that could obtained by malicious agents, or simply communication delay. In Section 7.3, we show how multi-level coordination fails to reduce communication delay for the manufacturing domain example but, for other domains, can be expected to reduce communication overhead exponentially.

7.1 Coordinated Planning Experiments

In this section, we describe experiments that evaluate the use of summary information in coordinating a group of evacuation transports that must together retrieve evacuees from a number of locations with constraints on the routes. In comparing the EMTF and CFTF search techniques described in Section 5.2 against conventional HTN approaches, the experiments show that reasoning about summary information finds optimally coordinated plans much more quickly than prior HTN techniques.

We compare different techniques for ordering the expansion of subplans of both $and$ and $or$ plans to direct the decomposition of plan hierarchies in the search for optimal solutions. These expansion techniques are the $expand$ (for $and$ subplans) and $select$ (for $or$ subplans) operators of the algorithm described in Section 5.1.

We compare EMTF's expansion of $and$ plans to the ExCon heuristic and to a random selection heuristic. The ExCon heuristic [Tsuneto, Hendler, Nau, 1998] first selects plans that can achieve an external precondition, or if there are no such plans, it selects one that threatens the external precondition. In the case that there are neither achieving or threatening plans, it chooses randomly. Note that EMTF will additionally choose to expand plans with only threatened external preconditions but has no preference as to whether the plan achieves, threatens, or is threatened. For the expansion of $or$ plans, we compare CFTF to a depth-first (DFS) and a random heuristic.

We also compare the combination of CFTF and EMTF to an FAF (``fewest alternatives first'') heuristic and to the combination of DFS and ExCon. The FAF heuristic does not employ summary information but rather chooses to expand $and$ and select $or$ plans that have the fewest subplans [Currie Tate, 1991, Tsuneto, Hendler, Nau, 1997]. Since no summary information is used, threats are only resolved at primitive levels. While it has been shown that the FAF heuristic can be effectively used by an HTN planner [Tsuneto, Hendler, Nau, 1997], the combination of DFS and ExCon has been shown to make great improvements over FAF in a domain with more task interactions [Tsuneto, Hendler, Nau, 1998]. We show in one such domain that the CFTF and EMTF heuristics can together outperform combinations of FAF, DFS, and ExCon.

The problems were generated for an evacuation domain where transports are responsible for visiting certain locations along restricted routes to pick up evacuees and bring them back to safety points. Transports are allowed to be at the same location at the same time, but the coordinator must ensure that transports avoid collisions along the single lane routes. In addition, in order to avoid the risk of oncoming danger (from a typhoon or enemy attack), the transports must accomplish their goals as quickly as possible.

Figure 20: Evacuation problem

Suppose there are two transports, $t1$ and $t2$, located at safety points $s0$ and $s3$ respectively, and they must visit the locations 0, 1, and 2 and 2, 3, and 4 respectively and bring evacuees back to safe locations as shown in Figure 20. Because of overlap in the locations they must visit, the coordinator must synchronize their actions in order to avoid collision. The coordinator's goal network includes two unordered tasks, one for each transport to $evacuate$ the locations for which it is responsible. As shown in Figure 21, the high-level task for $t1$ ($evacuate$) decomposes into a primitive action of moving to location 0 on the ring and an abstract plan to traverse the ring ($make\ rounds$). $t1$ can travel in one direction around the ring without switching directions, or it can switch directions once. $t1$ can then either go clockwise or counterclockwise and, if switching, can switch directions at any location ($first\ route$) and travel to the farthest location it needs to visit from where it switched ($second\ route$). Once it has visited all the locations, it continues around until it reaches the first safety point in its path ($go\ back$ and $goto\ safe\ loc$). The $no\ move$ plan is for the case where $t1$ is already at location 0. The task for $t2$ can be refined similarly.

Figure 21: The plan hierarchy for transport $t1$

Suppose the coordinator gathers summary information for the plan hierarchy and attempts to resolve conflicts. Looking just at the summary information one level from the top, the coordinator can determine that if $t1$ finishes evacuating before $t2$ even begins, then there will be no conflicts since the external conditions of $t1$'s $evacuate$ plan are that none of the routes are being traversed. This solution has a makespan (total completion time) of 16 steps. The optimal solution is a plan of duration seven where $t1$ moves clockwise until it reaches location $s3$, and $t2$ starts out clockwise, switches directions at location 4, and then winds up at $s0$. For this solution $t1$ waits at location 2 for one time step to avoid a collision on the route from location 2 to location 3.

Figure 22: Comparing EMTF to random expansion in searching for optimal solutions

We generated problems with four, six, eight, and twelve locations; with two, three and four transports; and with no, some, and complete overlap in the locations the transports visit. Performance was measured as the number of search states expanded to find the optimal solution or (if the compared heuristics did not both find the optimal solution) as the number of states each expanded to find solutions of highest common quality within memory and time bounds. We chose this instead of CPU time as the measure of performance in order to avoid fairness issues with respect to implementation details of the various approaches.

Figure 23: Comparing EMTF to ExCon in searching for optimal solutions

The scatter plot in Figure 22 shows the relative performance of the combination of CFTF and EMTF (CFTF-EMTF) and the combination of CFTF and random $and$ expansion (CFTF-Rand). We chose scatterplots to compare results because they capture the results more simply than trying to plot against three dimensions of problem size/complexity. Note that for all scatter plots, the axes are scaled logarithmically. Points above the diagonal line mean that EMTF (x-axis) is performing better than Rand (y-axis) because fewer search states were required to find the optimal solution. While performance is similar for most problems, there are a few cases where CFTF-EMTF outperformed CFTF-Rand by an order of magnitude or more. Figure 23 exhibits a similar effect for CFTF-EMTF and CFTF-ExCon. Note that runs were terminated after the expansion of 3,500 search states. Data points at 3,500 (the ones forming a horizontal line at the top) indicate that no solution was found within memory and time constraints. While performance is similar for most problems, there are four points along the top where CFTF-ExCon finds no solution. Thus, although EMTF does not greatly improve performance for many problems, it rarely performs much worse, and almost always avoids getting stuck in fruitless areas of the search space compared to the ExCon and the random heuristic. This is to be expected since EMTF focuses on resolving conflicts among the most problematic plans first and avoids spending a lot of time reasoning about the details of less problematic plans.

Figure 24: Comparing CFTF and DFS in searching for optimal solutions

The combination of CFTF with EMTF, pruning inconsistent abstract plan spaces, and branch-and-bound pruning of more costly abstract plan spaces (all described in Section 5.2) much more dramatically outperforms techniques that do not reason at abstract levels. Figure 24 shows DFS-Rand expanding between one and three orders of magnitude more states than CFTF-Rand. Runs were terminated after the expansion of 25,000 search states. Data points at 25,000 (forming the horizontal line at the top) indicate that no solution was found within memory and time constraints. By avoiding search spaces with greater numbers conflicts, CFTF finds optimal or near-optimal solutions much more quickly. In Figures 25 and 26, CFTF-EMTF outperforms FAF-FAF (FAF for both selecting $and$ and $or$ plans) and DFS-ExCon by one to two orders of magnitude for most problems. These last two comparisons especially emphasize the importance of abstract reasoning for finding optimal solutions. Within a maximum of 3,500 expanded search states (the lowest cutoff point in the experiments), CFTF-EMTF and CFTF-Rand found optimal solutions for 13 of the 24 problems. CFTF-ExCon and FAF-FAF found 12; and DFS-ExCon and DFS-Rand only found three.

Figure 25: Comparing the use of summary information to the FAF heuristic

Figure 26: Comparing the use of summary information to the algorithm using external conditions

A surprising result is that FAF-FAF performs much better than DFS-ExCon for the evacuation problems contrary to the results given by tsuneto:98 that show DFS-ExCon dominating for problems with more goal interactions. We believe that this result was not reproduced here because those experiments involved hierarchies with no $or$ plans. The experiments show that the selection of $or$ subplans more greatly affects performance than the order of $and$ subplans to expand. So, we believe DFS-ExCon performed worse than FAF-FAF not because FAF is better at choosing $and$ subplans than ExCon but because FAF is stronger at selecting $or$ subplans than DFS.

However, the main point of this section is that each of the heuristic combinations that use summary information to find solutions and prune the search space at abstract levels (CFTF-EMTF, CFTF-ExCon, and CFTF-Rand) greatly outperform all of those that do not (FAF-FAF, DFS-ExCon, and DFS-Rand) when searching for optimal solutions.

7.2 Scheduling Experiments

The experiments we describe here show that summary information improves performance significantly when tasks within the same hierarchy have constraints over the same resource, and solutions are found at some level of abstraction. At the same time, there are cases where abstract reasoning incurs significant overhead when solutions are only found at deeper levels. However, in domains where decomposition choices are critical, we show that this overhead is insignificant because the CFTF heuristic chooses decompositions that more quickly lead to solutions at deeper levels. These experiments also show that the EMTF heuristic outperforms a simpler heuristic depending on the decomposition rate, raising new research questions. We use the ASPEN Planning System [Chien, Rabideu, Knight, Sherwood, Engelhardt, Mutz, Estlin, Smith, Fisher, Barrett, Stebbins, Tran, 2000b] to coordinate a rover team for the problem described next.

7.2.1 Problem Domains

The domain involves a team of rovers that must resolve conflicts over shared resources. We generate two classes of maps within which the rovers move. For one, we randomly generate a map of triangulated waypoints (Figure 27). For the other, we generate corridor paths from a circle of locations with three paths from the center to points on the circle to represent narrow paths around obstacles (Figure 28). This ``corridor'' map is used to evaluate the CFTF heuristic. We then select a subset of the points as science locations (where the rovers study rocks/soil) and use a simple multiple traveling salesman algorithm to assign routes for the rovers to traverse and perform experiments. The idea is that a map of the area around a lander is constructed from an image taken upon landing on Mars.

Figure 27: Randomly generated rectangular field of triangulated waypoints

Figure 28: Randomly generated waypoints along corridors

Paths between waypoints are assigned random capacities such that either one, two, or three rovers can traverse a path simultaneously. Only one rover can be at any waypoint, and rovers may not traverse paths in opposite directions at the same time. These constraints are modeled as metric resources. State variables are also used to ensure rovers are at locations from which they are about to leave. In addition, rovers must communicate with the lander for telemetry using a shared channel of fixed bandwidth (metric resource). Depending on the terrain between waypoints, the required bandwidth varies. 80 problems were generated for two to five rovers, three to six science locations per rover, and 9 to 105 waypoints. In general, problems that contain fewer waypoints and more science goals are more difficult because there are more interactions among the rovers.

Schedules consist of an abstract task for each rover that have an $and$ decomposition into tasks for visiting each assigned science location. Those tasks have an $or$ decomposition into the three shortest paths through the waypoints to the target science location. The paths have an $and$ decomposition into movements between waypoints. Additional levels of hierarchy were introduced for longer paths in order to keep the offline resource summarization tractable. Schedules ranged from 180 to 1300 tasks.

7.2.2 Empirical Results for Mars Rovers

We compare ASPEN using aggregation with and without summarization for three variations of the rectangular field domain. When using summary information, ASPEN also uses the EMTF and CFTF decomposition heuristics. One domain excludes the communications channel resource (no channel); one excludes the path capacity restrictions (channel only); and the other excludes neither (mixed). Since all of the movement tasks reserve the channel resource, greater improvement in performance is expected when using summary information according to the complexity analyses in Section 6.3. This is because constraints on the channel resource collapse in the summary information derived at higher levels such that any task in a hierarchy only has one constraint on the resource. When ASPEN does not use summary information, the hierarchies must be fully expanded, and the number of constraints on the channel resource is equivalent to the number of leaf movement tasks.

However, tasks within a rover's hierarchy rarely place constraints on the other path variables more than once, so the no channel domain corresponds to the worst case where summarization collapses no constraints. Here the complexity of moving an abstract task is the same without summary information for the fully expanded hierarchy as it is with summary information for a partially expanded hierarchy.

Figure 29 (top) exhibits two distributions of problems for the no channel domain. In most of the cases (points above the x=y diagonal), ASPEN with summary information finds a solution quickly at some level of abstraction. However, in many cases, summary information performs notably worse (points below the x=y diagonal). We discovered that for these problems finding a solution requires the planner to dig deeply into the rovers' hierarchies, and once it decomposes the hierarchies to the level of the solution, the difference in the additional time to find a solution between the two approaches is negligible (unless the use of summary information found a solution at a slightly higher level of abstraction more quickly). Thus, the time spent reasoning about summary information at higher levels incurred unnecessary overhead.

Figure 29: Plots for the a) no channel, b) mixed, and c) channel only domains

a)

b)

c)

But this is the worst case in the analysis in Section 6.3 where we showed that summary information had no advantage even if it found abstract solutions. So, why did summary information perform better when abstract solutions were found? It was not because of the CFTF heuristic since $or$ branch choices result in small differences in numbers of conflicts. It actually results from the stochastic nature of ASPEN's iterative repair. Although moving the most abstract tasks using aggregation without summary information would have enabled ASPEN to find solutions more quickly for fully expanded hierarchies, ASPEN must sometimes move lower level tasks independently of their parents and siblings in order to resolve conflicts at lower levels. The problem is that ASPEN has no heuristic to tell it at what level it needs to move activities, and it sometimes chooses to move activities at detailed levels unnecessarily. This search at lower levels is where the search space explodes. Using summary information to search at higher levels below lower levels of abstraction better protects ASPEN from unnecessary search.

Figure 29 (middle) shows significant improvement for summary information in the mixed domain compared to the no channel domain. Adding the channel resource rarely affects the use of summary information because the collapse in summary constraints incurs insignificant additional complexity. However, the channel resource makes the scheduling task noticeably more difficult for ASPEN when not using summary information. In the channel only domain (Figure 29 bottom), summary information finds solutions at the abstract level almost immediately, but the problems are still complicated when ASPEN does not use summary information. These results support the complexity analysis in Section 6.3 that argues that summary information exponentially improves performance when tasks within the same hierarchy have constraints over the same resource and when solutions are found at some level of abstraction.

Because summary information is generated offline, the domain modeler knows up front whether or not constraints are significantly collapsed. Thus, an obvious approach to avoiding cases where reasoning about summary information causes unnecessary overhead is to fully expand at the start of scheduling the hierarchies of tasks where summary information does not collapse. Because the complexity of moving a task hierarchy is the same in this case whether fully expanded or not, ASPEN does not waste time by duplicating its efforts at each level of expansion before reaching the level at which it finds a solution. Evaluating this approach is a subject of future work.

Earlier we mentioned that the CFTF heuristic is not effective for the rectangular field problems. This is because the choice among different paths to a science location usually does not make a significant difference in the number of conflicts encountered--if the rovers cross paths, all path choices usually still lead to conflict. For the set of corridor problems, path choices always lead down a different corridor to get to the target location, so there is usually a path that avoids a conflict and a path that causes one depending on the path choices of the other rovers. When ASPEN uses the CFTF heuristic, the performance dominates that of when it chooses decompositions randomly for all but two problems (Figure 30). This reflects experiments for the coordination algorithm in Section 7 that show that CFTF is crucial for reducing the search time required to find solutions.

Figure 30: Performance using the CFTF heuristic

In order to evaluate the EMTF heuristic for iterative repair planning, we compared it to a simple alternative. This alternative strategy (that we refer to as level decomposition) is to interleave repair with decomposition as separate steps. Step 1) The planner repairs the current schedule until the number of conflicts cannot be reduced. Step 2) It decomposes all abstract tasks one level down and returns to Step 1. By only spending enough time at a particular level of expansion that appears effective, the planner attempts to find the highest decomposition level where solutions exist without wasting time at any level. The time spent searching for a solution at any level of expansion is controlled by the rate at which abstract tasks are decomposed. The EMTF heuristic is implemented as a repair method to give priority to detailing plans that are involved in more conflicts.

Figure 31: Performance of EMTF vs. level-decomposition heuristics

Figure 31 shows the performance of EMTF vs. level decomposition for different rates of decomposition for three problems from the set with varied performance. The plotted points are averages over ten runs for each problem. Depending on the choice of rate of decomposition (the probability that a task will decompose when a conflict is encountered), performance varies significantly. However, the best decomposition rate can vary from problem to problem making it potentially difficult for the domain expert to choose. For example, for problem A in the figure, all tested decomposition rates for EMTF outperformed the use of level decomposition. At the same time, for problem C using either decomposition technique did not make a significant difference while for problem B choosing the rate for EMTF made a big difference in whether to use EMTF or level decomposition. Although these examples show varied performance, results for most other problems showed that a decomposition rate of around 15% was most successful. This suggests that a domain modeler may be able to choose a generally successful decomposition rate by running performance experiments for a set of example problems.⁸

We have demonstrated many of the results of the complexity analyses in Section 6. Scheduling with summary information gains speedups (over aggregation) by resolving conflicts at appropriate levels of abstraction. When summary information collapses, the scheduler gains exponential speedups. In addition, the CFTF heuristic enables exponential speedups when $or$ decomposition choices have varying numbers of conflicts.

7.3 Communication Overhead

Here we show that, depending on bandwidth, latency, and how summary information is communicated among the agents, delays due to communication overhead vary. If only communication costs are a concern, then at one extreme where message delay dominates cost, sending the plan hierarchy without summary information makes the most sense. At the other extreme where bandwidth costs dominate, it makes sense to send the summary information for each task in a separate message as each is requested. Still, there are cases when sending the summary information for tasks in groups makes the most sense. This section will explain how a system designer can choose how much summary information to send at a time in order to reduce communication overhead exponentially.

Consider a simple protocol where agents request coordination from a central coordinating agent. During the search for a feasible solution, whenever it decomposes a task, the coordinator requests summary information for the subtasks that it has not yet received. For the manufacturing domain, the coordinator may already have summary information for a task to move a part, but if it encounters a different instantiation of the same task schema, it still must request the parameters for the new task. If a coordinator needs the subplans of an $or$ plan, the client agent sends the required information for all subplans, specifying its preferences for each. The coordinator then chooses the most preferred subplan, and in the case it must backtrack, it chooses the next most preferred subplan. Once the coordinator finds a feasible solution, it sends modifications to each agent specifying which $or$ subplans are blocked and where the agent must send and wait for synchronization messages. An agent can choose to send summary information for some number of levels of expansion of the requested task's hierarchy.

For the manufacturing problem described in Section 1.1, communication data in terms of numbers of messages and the size of each was collected up to the point that the coordinator found the solution in Figure 13c. This data was collected for cases where agents sent summary information for tasks in their hierarchies, one at a time, two levels at a time, and all at once. The two levels include the requested task and its immediate subplans. The following table below summarizes the numbers and total sizes of messages sent for each granularity level of information:

Figure 32: Delay of communicating different granularities of summary information with varying a) latency and b) bandwidth

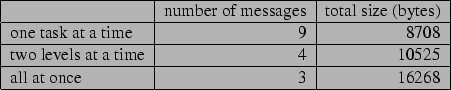
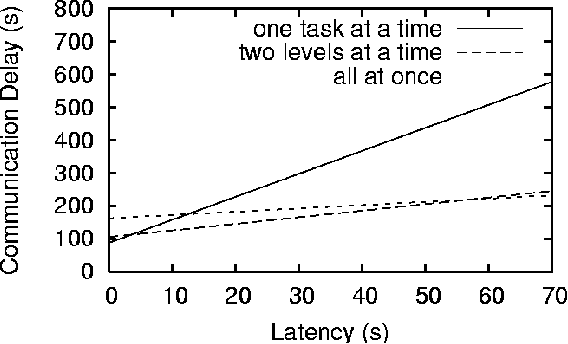a)

b)

Assuming that the coordinator must wait for requested information before continuing its search and can request only one task of one agent at a time, the coordination will be delayed for an amount of time depending on the bandwidth and latency of message passing. The total delay can be calculated as $(n-2)\ell + s/b$, where $n$ is the number of messages sent; $\ell$ is the latency in seconds; $s$ is the total size of all messages; and $b$ is the bandwidth in bytes per second. We use $n-2$ instead of $n$ because we assume that the agents all transmit their first top-level summary information message at the same time, so three messages actually only incur a delay of $\ell$ instead of $3\ell$.

Figure 32a shows how the communication delay varies for the three granularities of information for a fixed bandwidth of 100 bytes/second. (We will address the lack of realism in this example shortly.) When the latency is less than 3 seconds, sending summary information for each task in separate messages results in the smallest communication overhead. For latencies greater than 58 seconds, sending the entire hierarchy is best; and in between sending summary information two levels at a time is best. If the latency is fixed at 100 seconds, then the communication delay varies with bandwidth as shown in Figure 32b. When the bandwidth is less than 3 bytes/second, sending one at a time is best; sending it all at once is best for bandwidths greater than 60 bytes/second; and sending two levels at a time is best for bandwidths in between.

Admittedly, these values are unrealistic for the manufacturing domain. The manufacturing problem itself is very simple and provided mainly as an interesting domain for coordination. More realistic problems involving the manufacturing domain could have much larger hierarchies and require much larger scales of data to be sent. In that case more realistic bandwidth and latency values would exhibit similar tradeoffs.

To see this, suppose that the manufacturing managers' hierarchies had a common branching factor $b$ and depth $d$. If tasks generally had reservations on similar resources throughout the hierarchies, the amount of total summary information at a particular level would grow exponentially down the hierarchy just as would the number of tasks. If the agents agreed on a feasible solution at depth level $i$ in the hierarchy, then the table for messages and size would appear as follows:

Now suppose that the branching factor $b$ is 3; the depth $d$ is 10; the solution is found at level $i=5$; and the summary information for any task is 1 Kbyte. Then the table would look like this:

Figure 33: Delay with varying a) latency and b) bandwidth for hypothetical example

a)

b)

Now, if we fixed the bandwidth at 100 Kbyte/second and varied the latency, more realistic tradeoffs are seen in Figure 33a. Here, we see that unless the latency is very small, sending summary information two levels at a time is best. As shown in Figure 33b, if we fix latency to be one second and vary the bandwidth, for all realistic bandwidths sending summary information two levels at a time is again best.

This simple protocol illustrates how communication can be minimized by sending summary information at a particular granularity. If the agents chose not to send summary information but the unsummarized hierarchies instead, they would need to send their entire hierarchies. As the experiment shows, as hierarchies grow large, sending the entire hierarchy (``all at once'') would take a long time, even with a high bandwidth. Thus, using summary information (as opposed to not using it) can reduce communication exponentially when solutions can be found at abstract levels.

At the other extreme, if the agents sent summary information one task at a time, the latency for sending so many messages can grow large for larger task hierarchies. If solutions could only be found at primitive levels, then sending summary information one task at a time would cause an exponential latency overhead compared to sending the entire hierarchy at once. But, if solutions can be found at intermediate levels, being able to send summary information at some intermediate granularity can minimize total delay.

However, this argument assumes that summary information collapses at higher levels in the hierarchy. Otherwise, sending summary information at some intermediate level could be almost as expensive as sending the entire hierarchy and cause unnecessary overhead. For the actual manufacturing domain, tasks in the agents' hierarchies mostly have constraints on different resources, and summarization is not able to reduce summary information significantly because constraints do not collapse. The result is that it is better, in this case, to send the entire hierarchy at once to minimize delay (unless there are unusual bandwidth and latency constraints, as shown in the experiment). Even so, the coordination agent can still summarize the hierarchies itself to take advantage of the computational advantages of abstract reasoning.

This section showed how a domain modeler can minimize communication overhead by communicating summary information at the proper level of granularity. If bandwidth, latency, and a common depth for coordination solutions is known, the domain modeler can perform a hypothetical experiment like the one above for varying granularities of summary information to determine which granularity is optimal. If summary information collapses up the hierarchy, and solutions can be found at intermediate levels, then communication can be exponentially reduced in this manner.

8 Other Related Work

The approach we have taken for abstract reasoning was originally inspired by earlier work involving a hierarchical behavior-space search where agents represent their planned behaviors at multiple levels of abstraction [Durfee Montgomery, 1991]. Distributed protocols are used to decide at what level of abstraction coordination is needed and to resolve conflicts there. This approach capitalizes on domains where resources can be abstracted naturally. This earlier work can be viewed as a very limited, special case of the work presented here. It is justified only intuitively and with limited experiments and analyses.

Corkill studied interleaved planning and merging in a distributed version of the NOAH planner corkill:79. He recognized that, while most of the conditions affected by an abstract plan operator might be unknown until further refinement, those that deal with the overall effects and preconditions that hold no matter how the operator is refined can be captured and used to identify and resolve some conflicts. He recognized that further choices of refinement or synchronization choices at more abstract levels could lead to unresolvable conflicts at deeper levels, and backtracking could be necessary. Our work is directed toward avoiding such backtracking by using summary information to guide search.

In closer relation to our approach, Pappachan shows how to interleave hierarchical plan coordination with plan execution for cooperative agents using an online iterative constraint relaxation (OICR) algorithm [Pappachan, 2001]. Like our approach, coordination can be achieved at higher levels of abstraction for more flexible execution, or the agents can decompose their tasks to lower levels for tighter coordination that can improve plan quality. The OICR approach is tailored toward interleaving coordination and flexible execution at the price of completeness while the coordination algorithm presented here is aimed at complete interleaved coordination and planning at the price of potentially delaying execution due to backtracking.

In planning research, hierarchical plans have often been represented as Hierarchical Task Networks (HTNs, erol:94), which planners such as NOAH [Sacerdoti, 1977], NonLin [Tate, 1977], SIPE-2 [Wilkins, 1990], O-Plan [Currie Tate, 1991], UMCP [Erol, Nau, Hendler, 1994b], and SHOP2 [Nau, Au, Ilghami, Kuter, Murdock, Wu, Yaman, 2003] use to search through combinations of alternative courses of action to achieve goals within a particular context. These actions may be partially ordered, giving timing flexibility during execution [Wilkins, 1990, Currie Tate, 1991]. Our CHiP representation extends HTNs to include temporal extent and partial orderings can be expressed as constraints on the starting and ending timepoints of the action.

Yang presented a method (similar to our summarization) for preprocessing a plan hierarchy in order to be able to detect unresolvable conflicts at an abstract level so that the planner could backtrack from inconsistent search spaces [Yang, 1990]. This corresponds to the use of $\neg MightSomeWay$ in Section 5.2. However, his approach requires that the decomposition hierarchy be modeled so that each abstract operator have a unique main subaction that has the same preconditions and effects as the parent. We avoid this restriction by analyzing the subplans' conditions and ordering constraints to automatically compute the parent's summary conditions.

While our approach has focused on resolving conflicts among agents, cox:03 have used summary information to exploit synergistic interactions. The idea is that using summary information to identify overlapping effects can help agents skip actions whose effects are achieved by others. thang:03 have used summary information in rescheduling during execution. Their representations are actually subsumed by ours, and their work significantly postdates our first reporting of work in this paper [Clement Durfee, 1999].

DSIPE [desJardins Wolvertondes, 1999] is a distributed version of the SIPE-2 [Wilkins, 1990] hierarchical planning system. In the same way agents can use summary information to reduce communication to just those states for which they have common constraints, DSIPE filters conditions communicated among planners using irrelevance reasoning [Wolverton desJardins, 1998].

The DPOCL (Decompositional Partial-Order Causal-Link) planner [Young, Pollack, Moore, 1994] adds action decomposition to SNLP [Mc, 1991]. Like other HTN planners, preconditions and high level effects can be added to abstract tasks in order to help the planner resolve conflicts during decomposition. In addition, causal links can be specified in decomposition schemas to isolate external preconditions that DPOCL must satisfy. However, because these conditions and causal links do not necessarily capture all of the external conditions of abstract tasks, the planner does not find solutions at abstract levels and requires that all tasks be completely decomposed. In addition, DPOCL cannot determine that an abstract plan has unresolvable conflicts ($\neg MightSomeWay$) because there may be effects hidden in the decompositions of yet undetailed tasks that could achieve open preconditions. By deriving summary conditions automatically and using algorithms for determining causal link information (e.g. must-achieve), our planning/coordination algorithm can find and reject abstract plans during search without adding burden to the domain expert to specify redundant conditions or causal links for abstract tasks.

Like DPOCL, TÆMS (a framework for Task Analysis, Environment Modeling, and Simulation) allows the domain modeler to specify a wide range of task relationships [Decker, 1995]. This work offers quantitative methods for analyzing and simulating agents as well as their interactions. While only some of these interactions can be represented and discovered using summary conditions, we discover this information through analysis rather than depending on the model developer to predefine the interactions.

Grosz and Kraus's shared plans model of collaboration [Grosz Kraus, 1995] presents a theory for modeling multiagent belief and intention. While the shared plans work is directed toward cooperative agents, it represents action hierarchies and provides mental models at a higher level than represented in this article. However, our use and analysis of summary information complements Grosz's work by providing a way to automatically represent and efficiently reason about the intentions of agents at multiple levels of abstraction. Future work is needed to understand how summary information can be bridged with mental states of agents to exploit the techniques employed in shared plans and other work based on BDI (belief-desire-intention) models of agents [Rao Georgeff, 1995].

An analysis of hierarchical planning [Yang, 1997] explains that, in the case of interacting subgoals, certain structures of the hierarchy that minimize these interactions can reduce worst case planning complexity exponentially. However, the complexity analyses in Section 6 explain how using summary information can achieve exponential performance gains in addition to those achieved by restructuring plan hierarchies according to Yang's analysis by limiting the decomposition of task hierarchies and compressing the information manipulated by a coordinator, planner, or scheduler.

SHOP2 [Nau, Au, Ilghami, Kuter, Murdock, Wu, Yaman, 2003] is an HTN planner that uses a domain translation technique to reason about durative action. This however does not express temporal extent in the same way as the planner given here. Our model differs in that it supports ordering relationships on endpoints as well as conditions and effects during an action's execution. While there may be some domain translation that could achieve the expression of similar constraints and solutions for other systems, ours is the only formal model of such expressions in HTN planning.

SIADEX [Castillo, Fdez-Olivares, García-Pérez, Palao, 2006] is another HTN planner that handles temporal extent in the use of more expressive simple temporal networks [Dechter, Meiri, Pearl, 1991]. The performance improvement techniques reported for SIADEX are in temporal reasoning and not specific to HTNs. Thus, this work is complementary to ours. However, more work is needed to understand how summary information can be exploited in conjunction with the forward expansion approach that both SHOP2 and SIADEX use to perform competitively on planning competition problems.

Another class of hierarchical planners based on ABSTRIPS [Sacerdoti, 1974] introduces conditions at different levels of abstraction so that more critical conflicts are handled at higher levels of abstraction and less important (or easier) conflicts are resolved later at lower levels. While this approach similarly resolves conflicts at abstract levels, the planning decisions may not be consistent with conditions at lower levels resulting in backtracking. Summary information provides a means to make sound and complete decisions at abstract levels without the need to decompose and check consistency with lower levels. However, resolving conflicts based on criticality can still improve performance in complement to our approach.

Allen's temporal planner allen:91 uses hierarchical representations of tasks and could be applied to reasoning about the concurrent actions of multiple agents. However, it does not exploit hierarchy by reasoning about abstraction levels separately and generates a plan by proving the consistency of the collective constraints. Allen's model of temporal plans allen:83b and subsequent work on interval point algebra [Vilain Kautz, 1986] strongly influenced our hierarchical task representation and algorithms that reason about them.

There are also many, many models and theories of concurrency. Some older examples include automata representations, Petri nets and Hoare's theory of communicating sequential processes [Glabbeek, 1997]. There are also many temporal logics such as computational tree logic (CTL, ctl) that allow modal expressions about a proposition holding in some or all possible worlds some of the time, all of the time, in the next state, eventually, or until some other proposition holds. Another language for specifying manufacturing processes has been in the process of being standardized over 10 years [Bock, 1996, Schlenoff, Knutilla, Ray, 2006]. Many of these logics could have been used to define summary conditions and relations like $MightSomeWay$. However, we found that these logics were awkward for representing inconditions and defining summary conditions and that the terminology used in this article simplifies the definitions.

Model checking uses temporal logics to verify different properties of system models, software, and hardware (such as correctness, deadlock-free, and convergence). In fact, model checking and planning algorithms can be used interchangeably on the same problems []<e.g.,>giunchiglia:99. In the context of model checking, summary information is a set of properties (akin to those specifiable in CTL) of a system model (as a planning domain) that summarize system variable requirements (conditions) and assignments (effects). Thus, a model checking algorithm could use this summary information to efficiently identify and resolve potential requirement violations/bugs (condition conflicts) or deadlock (resource conflicts) in a system model or its operation (planning/scheduling problem instantiations).

9 Conclusion

This article provides a formalization of Hierarchical Task Network planning that, unlike the UMCP formalism [Erol, Nau, Hendler, 1994b], includes actions with temporal extent. We introduce a sound and complete algorithm that can be used to generate a plan, coordinate a group of agents with hierarchical plans, and interleave planning and coordination.

The algorithms for summarizing propositional state and metric resource conditions and effects at abstract levels and the mechanisms that reason about this summary information can facilitate the construction of other planning and coordination systems that reason about plans at multiple levels of abstraction. These mechanisms for reasoning about summary information determine whether a task (at any level of abstraction) must or may achieve, clobber, or undo a condition of another task under partial order constraints on endpoints of tasks. Built on these mechanisms, other mechanisms determine whether a group of agents can decompose and execute a set of partially ordered abstract tasks in any way ($CanAnyWay$), might decompose and execute them in some way ($MightSomeWay$), or cannot execute them consistently in any way ($\neg MightSomeWay$).

These algorithms enable a planning system to find solutions at multiple levels of abstraction without needing to fully detail the task hierarchy. These abstract solutions support flexible execution by remaining uncommitted about which of the alternative methods will be selected at runtime, based on the circumstances, to achieve plan subgoals.

Our complexity analyses and experiments in different problem domains have quantified the benefits of using summary information for a refinement planning and local search scheduling algorithm. There is a potential doubly exponential speedup of $O(k^{b^d-b^i} b^{2(d-i)})$ for $k$ ways to resolve a conflict, a hierarchy branching factor $b$, a depth of the hierarchy $d$, and an abstract solution depth $i$. An exponential speedup is obtained if abstract solutions are found, if there are fewer summary conditions at abstract levels, or if alternative decomposition choices lead to varying numbers of threats. These conditions for exponential improvement are a significant relaxation compared to prior work, and the performance improvement is greater.

A domain modeler can run the summarization algorithms offline for a library of plan hierarchies so that summary information is available for the coordination and planning of any set of goal tasks supported by the library. Using algorithms for reasoning about summary information, agents can discover with whom they should coordinate and over which states and resources they must coordinate/negotiate. Communicating summary information at different levels of abstraction reduces communication costs exponentially under conditions similar to those reducing computation time.

The use of summary information in a local search planner (like ASPEN, Section 6.3) is another contribution of this work. The strength of local search algorithms is their ability to efficiently reason about large numbers of tasks with constraints on metric resources, state variables, and other complex resource classes. By integrating algorithms for reasoning about summarized propositional state and metric resource constraints into a heuristic local search planner/scheduler, we enable such scalable planning systems to scale to even larger problem domains. This use of summary information in a different style of planner demonstrates the applicability of abstract reasoning in improving the performance of different kinds of planning (and plan coordination) systems.

Future work is needed to evaluate the use of summary information in other planning and scheduling systems and for wider classes of problems requiring more expressive representations for resources and temporal constraints. Already, an approach for exploiting cooperative action among agents based on summary information has been developed [Cox Durfee, 2003]. Other promising approaches include abstracting other plan information, such as probabilistic conditions and effects and classes of resources and states (e.g. location regions and sub-regions). More work is also needed to understand how and when to communicate summary information in a distributed planning system.

The authors wish to thank Pradeep Pappachan, Gregg Rabideau, and Russell Knight for help with implementation. We also thank our anonymous reviewers for their many valuable suggestions. This work was performed at the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration, and at the University of Michigan supported in part by DARPA (F30602-98-2-0142).

Appendix A: Algorithms for Computing Interval Relations

The algorithms for determining whether the defined relations hold between summary conditions for plans in $P$ use a point algebra constraint table [Vilain Kautz, 1986]. This point algebra table is constructed for the interval endpoints corresponding to the executions of the plans in $P$; a row and column for both $p^{-} \equiv t_s(e)$ (start endpoint of execution $e$ of $p$) and $p^{+} \equiv t_f(e)$ (finish endpoint) are added for each plan $p\in P$. Each cell of the table gives a time point constraint of the row to the column that can be $<$, $\leq$, $=$, $\geq$, $>$, $\neq$, $<=>$, or empty. $<=>$ means that the points are unconstrained. If a cell is empty, then there are no allowed temporal relations, indicating inconsistency. Table 1 shows a point algebra table for plans $p$ and $p'$ where they are constrained such that $p$'s execution contains that of $p'$. Table 2 shows a table where just the start of $p$ is constrained to be earlier than the start of $p'$. Both are transitive closures of these constraint relations. Table 1 can be computed from Table 2 by constraining $p^{+}<{p'}^{+}$ (by putting $<$ in the cell of row $p^{+}$ and column ${p'}^{+}$) and then computing the transitive closure, an $O(n^2)$ algorithm for $n$ points [Vilain Kautz, 1986]. After the transitive closure is computed, the constraints of any point on any other point can be looked up in constant time.

Table 1: Point algebra table for $p$ contains $p'$

Table 2: Point algebra table for $p^{-}$ before or at ${p'}^{-}$

Similarly, the constraints in $order$ for $P$ can be added to the table, and the transitive closure can be computed to get all constraints entailed from those in $order$. This only needs to be done once for any $P$ and $order$ to determine $achieve$ and $clobber$ relationships defined in the next section.

We determine that a plan $q$ in $p$'s subplans is temporally ordered always-[$first$,$last$] if and only if [$q^{-}$, $q^{+}$] is constrained [before, after] or equal to all other points in the point algebra table for $p$'s subplans. This is done by looking at each entry in the row for [$q^{-}$, $q^{+}$] and checking to see that the constraint is [$<$, $>$], $=$, or [$\leq$, $\geq$]. If this is not the case, then $q$ is not-always-[$first$,$last$]. $q$ is always-not-[$first$,$last$] if and only if in the row for [$q^{-}$, $q^{+}$] there is an entry with the [$>$, $<$] constraint; otherwise, it is sometimes-[$first$,$last$].

An interval $i_0$ is covered by a set of intervals $I=\{i_1,i_2,\ldots,i_k\}$ if and only no interval can be found that intersects $i_0$ and intersects nothing in $I$. Our particular covering problem describes the intervals in terms of a partial order over endpoints, so we represent these intervals in a point algebra table. An algorithm for the covering problem is to check to see if $i_0$ is covered by looking at all pairs of intervals to see if they overlap. $i_0$ is not covered if (1) either no intervals in $I$ meet either $i_0^{-}$ or $i_0^{+}$, (2) there are any intervals that have an endpoint that is contained only by $i_0$ and do not meet the opposite endpoint of another interval in $I$ or an endpoint of $i_0$, or (3) there are no intervals overlapping $i_0$. Otherwise, $i_0$ is covered. Examples are given in Figure 34.

Figure 34: a) Interval A is covered by B, C, and D. b) E is not covered by F, G, and H. c) I is not covered.

Appendix B: Algorithms for Must/May Asserting Summary Conditions

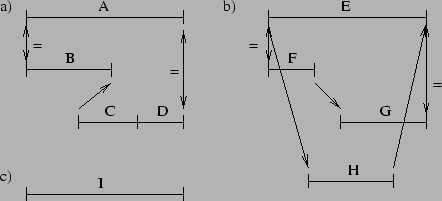Here we describe algorithms for determining temporal plan relationships based on summary information. They are used to build other algorithms that determine whether plan must or may achieve, clobber, or undo the condition of another under particular ordering constraints.

The definitions and algorithms throughout this section are given within the context of a set of plans $P$ with a corresponding set of summary information $P_{sum}$, a set of ordering constraints $order$, and a set of histories $H$ including all histories where $E(h)$ only includes an execution $e$ of each plan in $P$ and $e$'s subexecutions, and $E(h)$ satisfies all constraints in $order$. They are all concerned with the ordering of plan execution intervals and the timing of conditions. By themselves, they do not have anything to do with whether conditions may need to be met or must be met for a plan execution.

First, in order to determine whether abstract plan executions can achieve, clobber, or undo conditions of others, an agent needs to be able to reason about how summary conditions are asserted and required to be met. Ultimately, the agent needs to be able to determine whether a partial ordering of abstract plans can succeed, so it may be the case that an agent's action fails to assert a summary condition that is required by the action of another agent. Therefore, we formalize what it means for an action to attempt to assert a summary condition and to require that a summary condition be met. These definitions rely on linking the summary condition of a plan to the CHiP conditions it summarizes in the subplans of the plan's decompositions. Thus, we first define what it means for a summary condition to summarize these conditions.

Definition 14  

A summary condition $c$ summarizes a condition $\ell$ in condition set $conds$ of plan $p$ iff $c$ was added by the procedure for deriving summary information to a summary condition set of $p'$; $\ell=\ell(c)$; and either $c$ was added for $\ell$ in a condition set $conds$ of $p=p'$, or $c$ was added for a summary condition of a subplan of $p'$ that summarizes $\ell$ in $conds$ of $p$.

For example, $at$(bin1, A) is a precondition of the $start\_move$ plan for moving part A from bin1 to machine M1 (as given in Section 2.2). When deriving the summary conditions for $start\_move$, $at$(bin1, A) is added to the summary preconditions. Thus, the summary precondition $at$(bin1, A)MuF summarizes $at$(bin1, A) in the preconditions of $start\_move$.

Definition 15  

An execution $e$ of $p$ requires a summary condition $c$ to be met at $t$ iff $c$ is a summary condition in $p$'s summary information; there is a condition $\ell$ in a condition set $conds$ of $p'$ that is summarized by $c$; if $first(c)$, $t=t_s(e)$; if $last(c)$, $t=t_f(e)$; if $always(c)$, $t$ is within $(t_s(e), t_f(e))$; and if $sometimes(c)$, there is an execution of a subplan of $p$ in $d(e)$ that requires a summary condition $c'$ to be met at $t$, and $c'$ summarizes $\ell$ in $conds$ of $p'$.

So, basically, an execution requires a summary condition to be met whenever the conditions it summarizes are required. The execution of $build\_G$ has a summary precondition $at$(A,M1_tray1). This execution requires this summary condition to be met at $t_s$($build\_G$) because $at$(A, M1_tray1) is a precondition of $build\_G$'s first subplan that is summarized by $build\_G$'s summary precondition.

Definition 16  

An execution $e$ of $p$ attempts to assert a summary condition $c$ at $t$ iff $c$ is a summary condition in $p$'s summary information; there is a condition $\ell$ in a condition set $conds$ of $p'$ that is summarized by $c$; $\neg first(c)$; if $always(c)$, $t$ is in the smallest interval after $t_s(e)$ and before the start or end of any other execution that follows $t_s(e)$; if $last(c)$, $t=t_f(e)$; and if $sometimes(c)$, there is an execution of a subplan of $p$ in $d(e)$ that attempts to assert a summary condition $c'$ at $t$; and $c'$ summarizes $\ell$ in $conds$ of $p'$.

We say that an execution ``attempts'' to assert a summary condition because asserting a condition can fail due to a simultaneous assertion of the negation of the condition. Like the example above for requiring a summary condition, the executions of $build\_G$, $produce\_G\_on\_M1$, and $produce\_H$ all assert summary postconditions that M1 becomes available at $t_f$($build\_G$).

In order for agents to determine potential interactions among their abstract plans (such as clobbering or achieving), they need to reason about when a summary condition is asserted by one plan in relation to when it is asserted or required by another. Based on interval or point algebra constraints over a set of abstract plans, an agent specifically would need to be able to determine whether a plan would assert a summary condition before or by the time another plan requires or asserts a summary condition on the same state variable. In addition, to reason about clobbering inconditions, an agent would need to determine if a summary condition would be asserted during the time a summary incondition $c$ was required (asserted in $c$). Agents also need to detect when a summary postcondition would be asserted at the same time as another summary postcondition $c$ (asserted when $c$).

We do not consider cases where executions attempt to assert a summary in- or postcondition at the same time an incondition is asserted because in these cases, clobber relations are already detected because executions always require the summary inconditions that they attempt to assert. For example, if $equip\_M1$ attempted to assert the incondition that M1 was unavailable at the same time that $build\_G$ attempted to assert the postcondition that M1 was available, the incondition would be clobbered by the postcondition.

Table: Table for must-assert by/before algorithm

Table: Table for may-assert by/before algorithm

Table: Table for must/may-assert in algorithm

Table: Table for must/may-assert when algorithm

In the case that the ordering constraints allow for alternative synchronizations of the abstract plans, the assertions of summary conditions may come in different orders. Therefore, we formalize must-assert and may-assert to determine when these relationships must or may occur respectively. As mentioned at the beginning of Section 9, this use of ``must'' and ``may'' is based only on disjunctive orderings and not on the $existence$ of summary conditions in different decompositions. For the following definitions and algorithms of must- and may-assert, we assume $c$ and $c'$ are summary conditions of plans in $P$.

Definition 17  

$p'\in P$ must-assert $c'$ [by, before] $c$ iff for all histories $h\in H$ and all $t$ where $e$ is the top-level execution in $E(h)$ of some $p\in P$ that requires $c$ to be met at $t$, and $e'$ is the top-level execution of $p'$ in $E(h)$, there is a $t'$ where $e'$ attempts to assert $c'$ at $t'$, and [$t'\leq t$, $t'<t$].

The must-assert algorithm is described in Table 3. $p'$ must-assert $c'$ by $c$ iff $order$ entails the relationship given for the row corresponding to the type and timing of the two conditions. Rows of the table indicate the timing of both summary conditions and the constraints that $order$ must dictate for must-assert to be true. 'T' and 'F' in the table indicate whether the timing in the column is true or false for the condition. '?' means that timing doesn't matter for that condition in this case. For example, row 9 says that for the case where $c'$ is a $sometimes$ ($\neg last$) postcondition of $p'$, and $c$ is an incondition of $p$ with any timing, $order$ must require that the end of $p'$ be before or at the start of $p$ in order for $p'$ to must-assert $c'$ by the time $c$ is asserted or required.

The definitions and algorithms for the other assert relationships are similar. Tables 4-6 describe the logic for the other algorithms. For $may$ relationships, the algorithm returns true iff none of the corresponding ordering constraints in the table are imposed by (can be deduced from) $order$.

We illustrate these relationships for the example in Figure 8. In Figure 8a the agents' plans are unordered with respect to each other. Part G is produced either on machine M1 or M2 depending on potential decompositions of the $produce\_G$ plan. $produce\_G$ must-assert $c' = must$, $last$ $available$(G) before $c = must$, $first$ $available$(G) in the summary preconditions of $move\_G$ because no matter how the plans are decomposed (for all executions and all histories of the plans under the ordering constraints in the figure), the execution of $produce\_G$ attempts to assert $c'$ before the execution of $move\_G$ requires $c$ to be met. The algorithm verifies this by finding that the end of $produce\_G$ is ordered before the start of $move\_G$ (row 1 in Table 3). It is also the case that $equip\_M2\_tool$ may-assert $c' = must$, $last$ $\neg available$(M2) by $c = may$, $sometimes$ $available$(M2) in the summary preconditions of $produce\_G$ because the two plans are unordered with respect to each other, and in some history $equip\_M2\_tool$ can precede $produce\_G$. The algorithm finds that this is true since $equip\_M2$ is not constrained to start after the start of $produce\_G$ (row 2 in Table 4).

In Figure 8b, $move\_tool$ may-assert $c' = must$, $last$ $free$(transport1) in $c = may$, $sometimes$ $\neg free$(transport1) in $produce\_G$'s summary inconditions because in some history $move\_tool$ attempts to assert $c'$ during the time that $produce\_G$ is using transport1 to move part A to machine M2. In addition, $equip\_M2\_tool$ must-assert $c' = must$, $last$ $\neg available$(M2) when $c = may$, $last$ $available$(M2) in $produce\_G$'s summary postconditions because $equip\_M2\_tool$ attempts to assert $c'$ at the same time that $produce\_G$ requires $c$ to be met. The end of Section 3.3 gives other examples.

Bibliography

Allen, J., Kautz, H., Pelavin, R., Tenenberg, J. 1991.

Reasoning about plans.
Morgan Kaufmann.

Allen, J. F. 1983.

Maintaining knowledge about temporal intervals
Communications of the ACM, 26(11), 832-843.

Allen, J. F. Koomen, J. A. 1983.

Planning using a temporal world model
In Proceedings of the International Joint Conference on Artificial Intelligence, 741-747.

Bock, C. 1996.

Unified process specification language: Requirements for modeling process
NISTIR 5910, National Institute of Standards and Technology.

Castillo, L., Fdez-Olivares, J., García-Pérez, O., Palao, F. 2006.

Efficiently handling temporal knowledge in an HTN planner
In 16th International Conference on Automated Planning and Scheduling (ICAPS-06), 63-72. AAAI.

Chien, S., Knight, R., Stechert, A., Sherwood, R., Rabideau, G. 2000a.

Using iterative repair to improve the responsiveness of planning and scheduling
In Proceedings of the International Conference on AI Planning and Scheduling, 300-307.

Chien, S., Rabideu, G., Knight, R., Sherwood, R., Engelhardt, B., Mutz, D., Estlin, T., Smith, B., Fisher, F., Barrett, T., Stebbins, G., Tran, D. 2000b.

Automating space mission operations using automated planning and scheduling
In Proc. SpaceOps.

Clement, B. 2002.

Abstract Reasoning for Multiagent Coordination and Planning.
Ph.D. thesis, University of Michigan, Ann Arbor.

Clement, B. Durfee, E. 1999.

Top-down search for coordinating the hierarchical plans of multiple agents
In Proceedings of the International Conference on Autonomous Agents.

Corkill, D. 1979.

Hierarchical planning in a distributed environment
In Proceedings of the International Joint Conference on Artificial Intelligence, 168-175.

Cox, J. S. Durfee, E. H. 2003.

Discovering and exploiting synergy between hierarchical planning agents
In Proceedings of the International Joint Conference on Autonomous Agents and MultiAgent Systems, 281-288.

Currie, K. Tate, A. 1991.

O-Plan: The open planning architecture
Artificial Intelligence, 52, 49-86.

Decker, K. 1995.

Environment centered analysis and design of coordination mechanisms.
Ph.D. thesis, University of Massachusetts.

desJardins, M. Wolverton, M. 1999.

Coordinating a distributed planning system
AI Magazine, 20(4), 45-53.

Drabble, B. Tate, A. 1994.

The use of optimistic and pessimistic resource profiles to inform search in an activity based planner
In Artificial Intelligence Planning Systems, 243-248.

Durfee, E. H. Montgomery, T. A. 1991.

Coordination as distributed search in a hierarchical behavior space
IEEE Transactions of Systems, Man and Cybernetics, 21(6), 1363-1378.

Dechter, R., Meiri, I., Pearl, J. 1991.

Temporal constraint networks
Artificial Intelligence, 49, 61-95.

Emerson, E. Halpern, J. Y. 1985.

Decision procedures and expressiveness in the temporal logic of branching time
Journal of Computer and System Sciences, 30(1), 1-24.

Ephrati, E. Rosenschein, J. 1994.

Divide and conquer in multi-agent planning
In Proceedings of the National Conference on Artificial Intelligence, 375-380.

Erol, K., Hendler, J., Nau, D. 1994a.

Semantics for hierarchical task-network planning
CS-TR-3239, University of Maryland.

Erol, K., Nau, D., Hendler, J. 1994b.

UMCP: A sound and complete planning procedure for hierarchical task-network planning.
In Proceedings of the International Conference on AI Planning and Scheduling.

Fagin, R., Halpern, J., Moses, Y., Vardi, M. 1995.

Reasoning about knowledge.
MIT Press.

Firby, J. 1989.

Adaptive Execution in Complex Dynamic Domains.
Ph.D. thesis, Yale University.

Georgeff, M. P. 1983.

Communication and interaction in multiagent planning
In Proceedings of the National Conference on Artificial Intelligence, 125-129.

Georgeff, M. P. 1984.

A theory of action for multiagent planning
In Proceedings of the National Conference on Artificial Intelligence, 121-125.

Georgeff, M. P. Lansky, A. 1986.

Procedural knowledge
Proceedings of IEEE, 74(10), 1383-1398.

Giunchiglia, F. Traverso, P. 1999.

Planning as model checking
In Proceedings of the 5th European Conference on Planning, 1-20, London, UK. Springer-Verlag.

Glabbeek, R. v. 1997.

Notes on the methodology of CCS and CSP
Theoretical Computer Science, 177(2), 329-349.
Originally appeared as Report CS-R8624, CWI, Amsterdam, 1986.

Grosz, B. Kraus, S. 1996.

Collaborative plans for complex group action
Artificial Intelligence, 86, 269-358.

Huber, M. 1999.

JAM: A BDI-theoretic mobile agent architecture
In Proceedings of the International Conference on Autonomous Agents, 236-243.

Knight, R., Rabideau, G., Chien, S. 2000.

Computing valid intervals for collections of activities with shared states and resources
In Proceedings of the International Conference on AI Planning and Scheduling, 600-610.

Knoblock, C. 1991.

Search reduction in hierarchical problem solving
In Proceedings of the National Conference on Artificial Intelligence, 686-691.

Korf, R. 1987.

Planning as search: A quantitative approach
Artificial Intelligence, 33, 65-88.

Laborie, P. Ghallab, M. 1995.

Planning with sharable resource constraints
In Proceedings of the International Joint Conference on Artificial Intelligence, 1643-1649.

Lansky, A. 1990.

Localized search for controlling automated reasoning
In Proceedings of the DARPA Workshop on Innovative Approaches to Planning, Scheduling and Control, 115-125.

Lee, J., Huber, M. J., Durfee, E. H., Kenny, P. G. 1994.

UMPRS: An implementation of the procedural reasoning system for multirobot applications
In Proceedings of the AIAA/NASA Conference on Intelligent Robotics in Field, Factory, Service, and Space, 842-849.

McAllester, D. Rosenblitt, D. 1991.

Systematic nonlinear planning
In Proceedings of the National Conference on Artificial Intelligence, 634-639.

Muscettola, N. 1994.

HSTS: Integrating planning scheduling
Intelligent Scheduling, 169-212.

Nau, D., Au, T., Ilghami, O., Kuter, U., Murdock, J., Wu, D., Yaman, F. 2003.

SHOP2: An HTN planning system
Journal of Artificial Intelligence Research, 20, 379-404.

Pappachan, P. 2001.

Coordinating Plan Execution in Dynamic Multiagent Environments.
Ph.D. thesis, University of Michigan, Ann Arbor.

Pratt, V. R. 1976.

Semantical considerations on floyd-hoare logic
In 17th Annual IEEE Symposium on Foundations of Computer Science, 109-121.

Rao, A. S. Georgeff, M. P. 1995.

BDI-agents: From theory to practice
In Proceedings of the International Conference on Multi-Agent Systems, San Francisco.

Sacerdoti, E. 1974.

Planning in a hierarchy of abstraction spaces
Artificial Intelligence, 5(2), 115-135.

Sacerdoti, E. D. 1977.

A Structure for Plans and Behavior.
Elsevier-North Holland.

Schlenoff, C., Knutilla, A., Ray, S. 2006.

Interprocess communication in the process specification language
NISTIR 7348, National Institute of Standards and Technology.

Tate, A. 1977.

Generating project networks
In Proceedings of the International Joint Conference on Artificial Intelligence, 888-893.

Thangarajah, J., Padgham, L., Winikoff, M. 2003.

Detecting & avoiding interference between goals in intelligent agents
In Proceedings of the International Joint Conference on Artificial Intelligence, 721-726.

Tsuneto, R., Hendler, J., Nau, D. 1997.

Space-size minimization in refinement planning
In Proceedings of the European Conference on Planning.

Tsuneto, R., Hendler, J., Nau, D. 1998.

Analyzing external conditions to improve the efficiency of HTN planning
In Proceedings of the National Conference on Artificial Intelligence, 913-920.

Vilain Kautz, H. 1986.

Constraint propagation algorithms for temporal reasoning
In Proceedings of the National Conference on Artificial Intelligence, 377-382.

Weld, D. 1994.

An introduction to least commitment planning
AI Magazine, 15(4), 27-61.

Wilkins, D. E. 1990.

Can AI planners solve practical problems?
Computational Intelligence, 6(4), 232-246.

Wolverton, M. desJardins, M. 1998.

Controlling communication in distributed planning using irrelevance reasoning
In Proceedings of the National Conference on Artificial Intelligence, 868-874.

Yang, Q. 1990.

Formalizing planning knowledge for hierarchical planning
Computational Intelligence, 6(1), 12-24.

Yang, Q.. 1997.

Intelligent Planning: A Decomposition and Abstraction Based Approach.
Springer.

Young, M., Pollack, M., Moore, J. 1994.

Decomposition and causality in partial-order planning
In Proceedings of the International Conference on AI Planning and Scheduling, 188-193.

About this document ...

Abstract Reasoning for Planning and Coordination

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -html_version 3.0 -split 0 -toc_depth 4 -show_section_numbers -link 2 -long_titles 3 -white -dir jair06efinal_1_page jair06efinal.tex

The translation was initiated by Bradley Clement on 2006-12-29

Footnotes

....¹

Functions such as $pre(p)$ are used for referential convenience throughout this paper. Here, $pre$ and $pre(p)$ are the same, and $pre(p)$ is read as ``the preconditions of $p$.''

... conflict.²

Using universal quantification [Weld, 1994] a single plan could have a $\forall agent, agent \not=$ productionManager $\rightarrow \neg using$(transport1, $agent$) condition that would exclude concurrent access to the transport. We could have also simply specified transport1 as a non-consumable resource with maximum capacity of one.

... resource³

It is important not to confuse power with battery energy. A power source (e.g. battery, solar panels) makes a fixed amount of power in Watts available at any point in time. A battery's energy (in Watt-hours) is reduced by the integral of the total use of this power over time.

... subinterval⁴

For summary resource usages of the last interval intersecting the child task, we replace $[0,0]$ with $[e,f]$ in the $persist$.

... plans.⁵

In fact, it is NP-complete [Clement, 2002].

....⁶

This is why Georgeff chose to cluster multiple operators into ``critical regions'' and synchronize the (fewer) regions since there would be many fewer interleavings to check georgeff:83. By exploiting the hierarchical structure of plans, we use the ``clusters'' predefined in the hierarchy to this kind of advantage without needing to cluster from the bottom up.

... hierarchy.⁷

The analysis also applies to state constraints, but we restrict the discussion to resource usage constraints for simplicity.

... problems.⁸

For other experiments, we used a decomposition rate of 20% since it seemed to work well.