

Next: Non Planning Graph-based Heuristics
Up: Planning Graph Heuristics for
Previous: Summary of Methods for
This section discusses how we can use planning graph heuristics to
measure belief state distances. We cover several types of planning
graphs and the extent to which they can be used to compute various
heuristics. We begin with a brief background on planning graphs.
Planning Graphs: Planning graphs serve as the basis for our
belief state distance estimation. Planning graphs were initially
introduced in GraphPlan [4] for representing an
optimistic, compressed version of the state space progression tree.
The compression lies in unioning the literals from every state at
subsequent steps from the initial state. The optimism relates to
underestimating the number of steps it takes to support sets of
literals (by tracking only a subset of the infeasible tuples of
literals). GraphPlan searches the compressed progression (or
planning graph) once it achieves the goal literals in a level with
no two goal literals marked infeasible. The search tries to find
actions to support the top level goal literals, then find actions to
support the chosen actions and so on until reaching the first graph
level. The basic idea behind using planning graphs for search
heuristics is that we can find the first level of a planning graph
where a literal in a state appears; the index of this level is a
lower bound on the number of actions that are needed to achieve a
state with the literal. There are also techniques for estimating the
number of actions required to achieve sets of literals. The
planning graphs serve as a way to estimate the reachability of state
literals and discriminate between the ``goodness'' of different
search states. This work generalizes such literal estimations to
belief space search by considering both GraphPlan and CGP style
planning graphs plus a new generalization of planning graphs, called
the 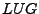 .
.
Planners such as CGP [30] and SGP [31]
adapt the GraphPlan idea of compressing the search space with a
planning graph by using multiple planning graphs, one for each
possible world in the initial belief state. CGP and SGP search on
these planning graphs, similar to GraphPlan, to find conformant and
conditional plans. The work in this paper seeks to apply the idea of
extracting search heuristics from planning graphs, previously used
in state space search
[23,18,5] to
belief space search.
Planning Graphs for Belief Space: This section proceeds by
describing four classes of heuristics to estimate belief state
distance
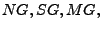 and
and 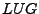 .
. 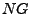 heuristics are techniques
existing in the literature that are not based on planning graphs,
heuristics are techniques
existing in the literature that are not based on planning graphs,
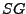 heuristics are techniques based on a single classical planning
graph,
heuristics are techniques based on a single classical planning
graph, 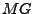 heuristics are techniques based on multiple planning
graphs (similar to those used in CGP) and
heuristics are techniques based on multiple planning
graphs (similar to those used in CGP) and 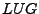 heuristics use a new
labelled planning graph. The
heuristics use a new
labelled planning graph. The 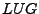 combines the advantages of
combines the advantages of 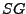 and
and 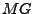 to reduce the representation size and maintain
informedness. Note that we do not include observations in any of
the planning graph structures as SGP [31] would, however we
do include this feature for future work. The conditional planning
formulation directly uses the planning graph heuristics by ignoring
observations, and our results show that this still gives good
performance.
to reduce the representation size and maintain
informedness. Note that we do not include observations in any of
the planning graph structures as SGP [31] would, however we
do include this feature for future work. The conditional planning
formulation directly uses the planning graph heuristics by ignoring
observations, and our results show that this still gives good
performance.
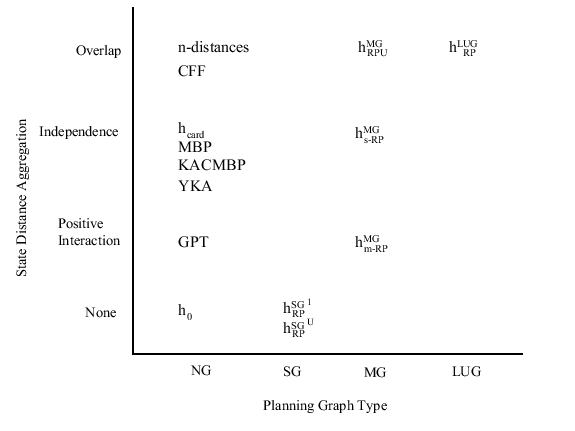
Figure 4:
Taxonomy of heuristics with respect to planning graph type and
state distance aggregation. Blank entries indicate that the
combination is meaningless or not possible.
|
In Figure 4 we present a taxonomy of distance measures
for belief space. The taxonomy also includes related planners,
whose distance measures will be characterized in this section. All
of the related planners are listed in the 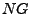 group, despite the
fact that some actually use planning graphs, because they do not
clearly fall into one of our planning graph categories. The figure
shows how different substrates (horizontal axis) can be used to
compute belief state distance by aggregating state to state
distances under various assumptions (vertical axis). Some of the
combinations are not considered because they do not make sense or
are impossible. The reasons for these omissions will be discussed
in subsequent sections. While there are a wealth of different
heuristics one can compute using planning graphs, we concentrate on
relaxed plans because they have proven to be the most effective in
classical planning and in our previous studies [9].
We provide additional descriptions of other heuristics like max,
sum, and level in Appendix A.
group, despite the
fact that some actually use planning graphs, because they do not
clearly fall into one of our planning graph categories. The figure
shows how different substrates (horizontal axis) can be used to
compute belief state distance by aggregating state to state
distances under various assumptions (vertical axis). Some of the
combinations are not considered because they do not make sense or
are impossible. The reasons for these omissions will be discussed
in subsequent sections. While there are a wealth of different
heuristics one can compute using planning graphs, we concentrate on
relaxed plans because they have proven to be the most effective in
classical planning and in our previous studies [9].
We provide additional descriptions of other heuristics like max,
sum, and level in Appendix A.
Example: To illustrate the computation of each heuristic, we
use an example derived from BTC called Courteous BTC (CBTC) where a
courteous package dunker has to disarm the bomb and leave the toilet
unclogged, but some discourteous person has left the toilet clogged.
The initial belief state of CBTC in clausal representation is:
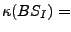 arm
arm  clog
clog  (inP1
(inP1 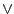 inP2)
inP2)  (
(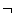 inP1
inP1  inP2),
inP2),
and the goal is:
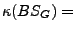
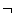 clog
clog
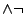 arm.
arm.
The optimal action sequences to reach 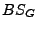 from
from  are:
are:
Flush, DunkP1, Flush, DunkP2, Flush,
and
Flush, DunkP2, Flush, DunkP1, Flush.
Thus the optimal heuristic estimate for the distance
between  and
and 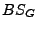 , in regression, is
, in regression, is
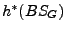 = 5
because in either plan there are five actions.
= 5
because in either plan there are five actions.
We use planning graphs for both progression and regression search.
In regression search the heuristic estimates the cost of the current
belief state w.r.t. the initial belief state and in progression
search the heuristic estimates the cost of the goal belief state
w.r.t. the current belief state. Thus, in regression search the
planning graph(s) are built (projected) once from the possible
worlds of the initial belief state, but in progression search they
need to be built at each search node. We introduce a notation
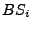 to denote the belief state for which we find a heuristic
measure, and
to denote the belief state for which we find a heuristic
measure, and 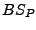 to denote the belief state that is used to
construct the initial layer of the planning graph(s). In the
following subsections we describe computing heuristics for
regression, but they are generalized for progression by changing
to denote the belief state that is used to
construct the initial layer of the planning graph(s). In the
following subsections we describe computing heuristics for
regression, but they are generalized for progression by changing
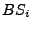 and
and 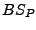 appropriately.
appropriately.
In the previous section we discussed two important issues involved
in heuristic computation: sampling states to include in the
computation and using mutexes to capture negative interactions in
the heuristics. We will not directly address these issues in this
section, deferring them to discussion in the respective empirical
evaluation sections, 6.4 and 6.2. The heuristics below are computed
once we have decided on a set of states to use, whether by sampling
or not. Also, as previously mentioned, we only consider sampling
states from the belief state 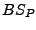 because we can implicitly find
closest states from
because we can implicitly find
closest states from 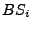 without sampling. We only explore
computing mutexes on the planning graphs in regression search. We
use mutexes to determine the first level of the planning graph where
the goal belief state is reachable (via the level heuristic
described in Appendix A) and then extract a relaxed plan starting at
that level. If the level heuristic is
without sampling. We only explore
computing mutexes on the planning graphs in regression search. We
use mutexes to determine the first level of the planning graph where
the goal belief state is reachable (via the level heuristic
described in Appendix A) and then extract a relaxed plan starting at
that level. If the level heuristic is 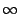 because there is no
level where a belief state is reachable, then we can prune the
regressed belief state.
because there is no
level where a belief state is reachable, then we can prune the
regressed belief state.
We proceed by describing the various substrates used for computing
belief space distance estimates. Within each we describe the
prospects for various types of world aggregation. In addition to
our heuristics, we mention related work in the relevant areas.
Subsections


Next: Non Planning Graph-based Heuristics
Up: Planning Graph Heuristics for
Previous: Summary of Methods for
2006-05-26
