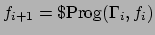Having defined a language to represent behaviours to be rewarded, we
now turn to the problem of computing, given a reward formula, a
minimum allocation of rewards to states actually encountered in an
execution sequence, in such a way as to satisfy the formula. Because
we ultimately wish to use anytime solution methods which generate
state sequences incrementally via forward search, this computation is
best done on the fly, while the sequence is being generated. We
therefore devise an incremental algorithm based on a model-checking
technique normally used to check whether a state sequence is a model
of an FLTL formula [4]. This technique is known
as formula progression because it `progresses' or `pushes' the
formula through the sequence.
Our progression technique is shown in Algorithm 1.
In essence, it computes the modelling relation
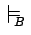 given in
Section 3.2. However,unlike the definition of
given in
Section 3.2. However,unlike the definition of
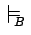 , it is designed to be useful when states in the sequence
become available one at a time, in that it defers the evaluation of
the part of the formula that refers to the future to the point where
the next state becomes available. Let
, it is designed to be useful when states in the sequence
become available one at a time, in that it defers the evaluation of
the part of the formula that refers to the future to the point where
the next state becomes available. Let 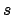 be a state, say
be a state, say 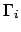 ,
the last state of the sequence prefix
,
the last state of the sequence prefix 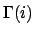 that has been
generated so far, and let
that has been
generated so far, and let 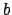 be a boolean true iff
be a boolean true iff 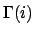 is in
the behaviour
is in
the behaviour 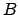 to be rewarded. Let the
to be rewarded. Let the
 formula
formula  describe the allocation of rewards over all possible futures. Then the
progression of
describe the allocation of rewards over all possible futures. Then the
progression of  through
through 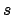 given
given 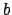 , written
, written
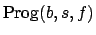 , is a
new formula which will describe the allocation of rewards over all
possible futures of the next state, given that we have just
passed through
, is a
new formula which will describe the allocation of rewards over all
possible futures of the next state, given that we have just
passed through 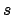 . Crucially, the function
. Crucially, the function  is Markovian,
depending only on the current state and the single boolean value
is Markovian,
depending only on the current state and the single boolean value 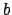 .
Note that
.
Note that  is computable in linear time in the length of
is computable in linear time in the length of  ,
and that for $-free formulae, it collapses to FLTL formula
progression [4], regardless of the value of
,
and that for $-free formulae, it collapses to FLTL formula
progression [4], regardless of the value of 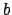 .
We assume that Prog incorporates the usual simplification for
sentential constants
.
We assume that Prog incorporates the usual simplification for
sentential constants  and
and 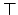 :
:
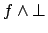 simplifies to
simplifies to 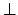 ,
,
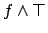 simplifies to
simplifies to  , etc.
, etc.

The fundamental property of  is the following. Where
is the following. Where
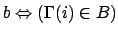 :
:
Proof:
See Appendix B. 
Like
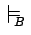 , the function
, the function  seems to require
seems to require 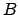 (or at
least
(or at
least 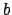 ) as input, but of course when progression is applied in
practice we only have
) as input, but of course when progression is applied in
practice we only have  and one new state at a time of
and one new state at a time of  , and
what we really want to do is compute the appropriate
, and
what we really want to do is compute the appropriate 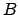 , namely
that represented by
, namely
that represented by  . So, similarly as in
Section 3.2, we now turn to the second step, which
is to use
. So, similarly as in
Section 3.2, we now turn to the second step, which
is to use  to decide on the fly whether a newly generated
sequence prefix
to decide on the fly whether a newly generated
sequence prefix 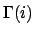 is in
is in 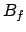 and so should be allocated a
reward. This is the purpose of the functions
and so should be allocated a
reward. This is the purpose of the functions
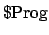 and
and
 , also given in Algorithm 1. Given
, also given in Algorithm 1. Given  and
and  , the function
, the function
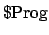 in
Algorithm 1 defines an infinite sequence of
formulae
in
Algorithm 1 defines an infinite sequence of
formulae
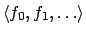 in the obvious way:
in the obvious way:

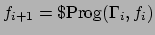
To decide whether a prefix 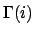 of
of  is to be rewarded,
is to be rewarded,
 first tries progressing the formula
first tries progressing the formula 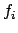 through
through 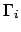 with the boolean flag set to `false'. If that gives a consistent
result, we need not reward the prefix and we continue without
rewarding
with the boolean flag set to `false'. If that gives a consistent
result, we need not reward the prefix and we continue without
rewarding 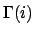 , but if the result is
, but if the result is 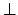 then we know that
then we know that
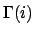 must be rewarded in order for
must be rewarded in order for  to satisfy
to satisfy  . In
that case, to obtain
. In
that case, to obtain 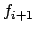 we must progress
we must progress 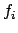 through
through
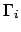 again, this time with the boolean flag set to the value
`true'. To sum up, the behaviour corresponding to
again, this time with the boolean flag set to the value
`true'. To sum up, the behaviour corresponding to  is
is
 .
To illustrate the behaviour of $FLTL progression, consider the
formula
.
To illustrate the behaviour of $FLTL progression, consider the
formula
![$f = \neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p \wedge \mbox{\$})$](img268.png) stating that a reward
will be received the first time
stating that a reward
will be received the first time 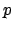 is true. Let
is true. Let 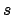 be a state in
which
be a state in
which 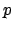 holds, then
holds, then
![$\mbox{Prog}(\mbox{false},s,f) = \bot \vee (\bot
\wedge \neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p \wedge \mbox{\$})) \equiv \bot$](img269.png) . Therefore,
since the formula has progressed to
. Therefore,
since the formula has progressed to  ,
,
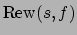 is true and a reward is received.
is true and a reward is received.
![$\mbox{\$}\mbox{Prog}(s,f) = \mbox{Prog}(\mbox{true},s,f) = \top \vee (\bot \wedge
\neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p \wedge \mbox{\$})) \equiv \top$](img272.png) , so the reward formula
fades away and will not affect subsequent progression steps. If, on
the other hand,
, so the reward formula
fades away and will not affect subsequent progression steps. If, on
the other hand, 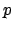 is false in
is false in 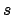 , then
, then
![$\mbox{Prog}(\mbox{false},s,f) =
\bot \vee (\top \wedge \neg p \makebox[1em]{$\m...
...$})) \equiv \neg p
\makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p \wedge \mbox{\$}))$](img273.png) . Therefore, since the formula has not
progressed to
. Therefore, since the formula has not
progressed to  ,
,
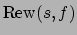 is false and no reward is received.
is false and no reward is received.
![$\mbox{\$}\mbox{Prog}(s,f) =
\mbox{Prog}(\mbox{false},s,f) = \neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p \wedge \mbox{\$})$](img274.png) , so the
reward formula persists as is for subsequent progression steps.
The following theorem states that under weak assumptions, rewards are
correctly allocated by progression:
, so the
reward formula persists as is for subsequent progression steps.
The following theorem states that under weak assumptions, rewards are
correctly allocated by progression:
Theorem 1
Let  be reward-normal, and let
be reward-normal, and let
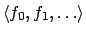 be the result of progressing it through the successive states of a
sequence
be the result of progressing it through the successive states of a
sequence  using the function
using the function
 .
Then, provided no
.
Then, provided no 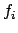 is
is
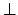 , for all
, for all 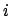
 iff
iff
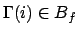 .
.
Proof: See Appendix B 
The premise of the theorem is that  never progresses to
never progresses to
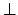 . Indeed if
. Indeed if
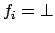 for some
for some 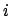 , it means that even
rewarding
, it means that even
rewarding 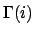 does not suffice to make
does not suffice to make  true, so something
must have gone wrong: at some earlier stage, the boolean
true, so something
must have gone wrong: at some earlier stage, the boolean  was
made false where it should have been made true. The usual explanation
is that the original
was
made false where it should have been made true. The usual explanation
is that the original  was not reward-normal. For instance
was not reward-normal. For instance
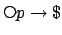 , which is reward unstable, progresses to
, which is reward unstable, progresses to 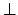 in
the next state if p is true there: regardless of
in
the next state if p is true there: regardless of 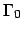 ,
,
 ,
,
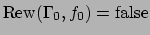 , and
, and
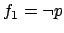 , so if
, so if
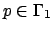 then
then
 . However, other (admittedly
bizarre) possibilities exist: for example, although
. However, other (admittedly
bizarre) possibilities exist: for example, although
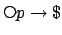 is reward-unstable, its substitution instance
is reward-unstable, its substitution instance
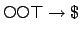 , which also progresses to
, which also progresses to  in a few steps, is logically equivalent to
in a few steps, is logically equivalent to  and is
reward-normal.
If the progression method were to deliver the correct minimal behaviour
in all cases (even in all reward-normal cases) it would have to
backtrack on the choice of values for the boolean flags. In the
interest of efficiency, we choose not to allow backtracking. Instead,
our algorithm raises an exception whenever a reward formula progresses
to
and is
reward-normal.
If the progression method were to deliver the correct minimal behaviour
in all cases (even in all reward-normal cases) it would have to
backtrack on the choice of values for the boolean flags. In the
interest of efficiency, we choose not to allow backtracking. Instead,
our algorithm raises an exception whenever a reward formula progresses
to  , and informs the user of the sequence which caused the
problem. The onus is thus placed on the domain modeller to select
sensible reward formulae so as to avoid possible progression to
, and informs the user of the sequence which caused the
problem. The onus is thus placed on the domain modeller to select
sensible reward formulae so as to avoid possible progression to  .
It should be noted that in the worst case, detecting reward-normality
cannot be easier than the decision problem for $FLTL so it is not to
be expected that there will be a simple syntactic criterion for
reward-normality.
In practice, however, commonsense precautions such as avoiding making
rewards depend explicitly on future tense expressions suffice to keep
things normal in all routine cases. For a generous class of
syntactically recognisable reward-normal formulae, see Appendix
A.
Sylvie Thiebaux
2006-01-20
.
It should be noted that in the worst case, detecting reward-normality
cannot be easier than the decision problem for $FLTL so it is not to
be expected that there will be a simple syntactic criterion for
reward-normality.
In practice, however, commonsense precautions such as avoiding making
rewards depend explicitly on future tense expressions suffice to keep
things normal in all routine cases. For a generous class of
syntactically recognisable reward-normal formulae, see Appendix
A.
Sylvie Thiebaux
2006-01-20