Examples
It is intuitively clear that many behaviours can be specified by means
of $FLTL formulae. While there is no simple way in general to
translate between past and future tense expressions,4all of the examples used to illustrate PLTL in
Section 2.2 above are expressible naturally in
$FLTL, as follows.
The classical goal formula 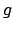 saying that a goal
saying that a goal 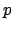 is rewarded
whenever it happens is easily expressed:
is rewarded
whenever it happens is easily expressed:
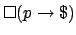 . As already noted,
. As already noted, 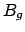 is the set of finite sequences of
states such that
is the set of finite sequences of
states such that 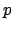 holds in the last state. If we only care that
holds in the last state. If we only care that 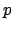 is achieved once and get rewarded at each state from then on, we write
is achieved once and get rewarded at each state from then on, we write
 . The behaviour that this formula
represents is the set of finite state sequences having at least one
state in which
. The behaviour that this formula
represents is the set of finite state sequences having at least one
state in which 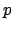 holds. By contrast, the formula
holds. By contrast, the formula
![$\neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}(p
\wedge \mbox{\$})$](img239.png) stipulates only that the first occurrence of
stipulates only that the first occurrence of 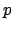 is
rewarded (i.e. it specifies the behaviour in Figure 1).
To reward the occurrence of
is
rewarded (i.e. it specifies the behaviour in Figure 1).
To reward the occurrence of 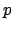 at most once every
at most once every 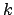 steps, we write
steps, we write
 .
For response formulae, where the achievement of
.
For response formulae, where the achievement of 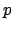 is triggered by
the command
is triggered by
the command 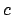 , we write
, we write
 to reward every state in which
to reward every state in which 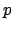 is true following the
first issue of the command. To reward only the first occurrence
is true following the
first issue of the command. To reward only the first occurrence 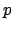 after each command, we write
after each command, we write
![$\mbox{$\Box$}(c\rightarrow \raisebox{0.6mm}{$\scriptstyle \bigcirc$}(\neg p \makebox[1em]{$\mathbin{\mbox{\sf U}}$}
(p \wedge \mbox{\$})))$](img242.png) . As for bounded variants for which we only
reward goal achievement within
. As for bounded variants for which we only
reward goal achievement within 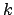 steps of the trigger command, we
write for example
steps of the trigger command, we
write for example
 to reward all such states in which
to reward all such states in which 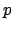 holds.
It is also worth noting how to express simple behaviours involving
past tense operators. To stipulate a reward if
holds.
It is also worth noting how to express simple behaviours involving
past tense operators. To stipulate a reward if 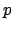 has always been
true, we write
has always been
true, we write
![$\mbox{\$}\makebox[1em]{$\mathbin{\mbox{\sf U}}$}\neg p$](img244.png) . To say that we are rewarded if
. To say that we are rewarded if
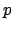 has been true since
has been true since 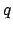 was, we write
was, we write
![$\mbox{$\Box$}(q \rightarrow (\mbox{\$}
\makebox[1em]{$\mathbin{\mbox{\sf U}}$}\neg p))$](img245.png) .
Finally, we often find it useful to reward the holding of
.
Finally, we often find it useful to reward the holding of 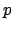 until
the occurrence of
until
the occurrence of 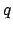 . The neatest expression for this is
. The neatest expression for this is
![$\neg q
\makebox[1em]{$\mathbin{\mbox{\sf U}}$}((\neg p \wedge \neg q) \vee (q \wedge \mbox{\$}))$](img246.png) .
Sylvie Thiebaux
2006-01-20
.
Sylvie Thiebaux
2006-01-20