The main drawback of traditional dynamic programming algorithms such
as policy iteration [32] is that they explicitly
enumerate all states that are reachable from  in the entire
MDP. There has been interest in other state-based solution methods,
which may produce incomplete policies, but only enumerate a fraction
of the states that policy iteration requires.
Let
in the entire
MDP. There has been interest in other state-based solution methods,
which may produce incomplete policies, but only enumerate a fraction
of the states that policy iteration requires.
Let  denote the envelope of policy
denote the envelope of policy 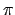 , that is the
set of states that are reachable (with a non-zero probability) from
the initial state
, that is the
set of states that are reachable (with a non-zero probability) from
the initial state  under the policy. If
under the policy. If 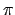 is defined at all
is defined at all
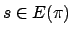 , we say that the policy is complete, and that it
is incomplete otherwise. The set of states in
, we say that the policy is complete, and that it
is incomplete otherwise. The set of states in  at which
at which
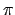 is undefined is called the fringe of the policy. The
fringe states are taken to be absorbing, and their value is heuristic.
A common feature of anytime state-based algorithms is that they perform a
forward search, starting from
is undefined is called the fringe of the policy. The
fringe states are taken to be absorbing, and their value is heuristic.
A common feature of anytime state-based algorithms is that they perform a
forward search, starting from  and repeatedly expanding the
envelope of the current policy one step forward by adding one or more
fringe states. When provided with admissible heuristic values for the
fringe states, they eventually converge to the optimal policy without
necessarily needing to explore the entire state space. In fact, since
planning operators are used to compactly represent the state space,
they may not even need to construct more than a small subset of
the MDP before returning the optimal policy. When interrupted before
convergence, they return a possibly incomplete but often useful
policy.
These methods include the envelope expansion algorithm
[17], which deploys policy iteration on judiciously
chosen larger and larger envelopes, using each successive policy to
seed the calculation of the next. The more recent LAO
and repeatedly expanding the
envelope of the current policy one step forward by adding one or more
fringe states. When provided with admissible heuristic values for the
fringe states, they eventually converge to the optimal policy without
necessarily needing to explore the entire state space. In fact, since
planning operators are used to compactly represent the state space,
they may not even need to construct more than a small subset of
the MDP before returning the optimal policy. When interrupted before
convergence, they return a possibly incomplete but often useful
policy.
These methods include the envelope expansion algorithm
[17], which deploys policy iteration on judiciously
chosen larger and larger envelopes, using each successive policy to
seed the calculation of the next. The more recent LAO algorithm
[28] which combines dynamic programming with
heuristic search can be viewed as a clever implementation of a
particular case of the envelope expansion algorithm, where fringe
states are given admissible heuristic values, where policy iteration
is run up to convergence between envelope expansions, and where the
clever implementation only runs policy iteration on the states whose
optimal value can actually be affected when a new fringe state is
added to the envelope. Another example is a backtracking forward
search in the space of (possibly incomplete) policies rooted at
algorithm
[28] which combines dynamic programming with
heuristic search can be viewed as a clever implementation of a
particular case of the envelope expansion algorithm, where fringe
states are given admissible heuristic values, where policy iteration
is run up to convergence between envelope expansions, and where the
clever implementation only runs policy iteration on the states whose
optimal value can actually be affected when a new fringe state is
added to the envelope. Another example is a backtracking forward
search in the space of (possibly incomplete) policies rooted at
 [45], which is performed until interrupted,
at which point the best policy found so far is returned. Real-time
dynamic programming (RTDP) [8] is another popular
anytime algorithm which is to MDPs what learning real-time A
[45], which is performed until interrupted,
at which point the best policy found so far is returned. Real-time
dynamic programming (RTDP) [8] is another popular
anytime algorithm which is to MDPs what learning real-time A [36] is to deterministic domains, and which has asymptotic
convergence guarantees. The RTDP envelope is made up of sample paths
which are visited with a frequency determined by the current greedy
policy and the transition probabilities in the domain. RTDP can be
run on-line, off-line for a given number of steps or until
interrupted. A variant called LRTDP [9] incorporates mechanisms that focus the search on states whose value
has not yet converged, resulting in convergence speed up and finite
time convergence guarantees.
The FLTL translation we are about to present targets these anytime
algorithms, although it could also be used with more
traditional methods such as value and policy iteration.
Sylvie Thiebaux
2006-01-20
[36] is to deterministic domains, and which has asymptotic
convergence guarantees. The RTDP envelope is made up of sample paths
which are visited with a frequency determined by the current greedy
policy and the transition probabilities in the domain. RTDP can be
run on-line, off-line for a given number of steps or until
interrupted. A variant called LRTDP [9] incorporates mechanisms that focus the search on states whose value
has not yet converged, resulting in convergence speed up and finite
time convergence guarantees.
The FLTL translation we are about to present targets these anytime
algorithms, although it could also be used with more
traditional methods such as value and policy iteration.
Sylvie Thiebaux
2006-01-20