The syntax of PLTL, the language chosen to represent rewarding
behaviours, is that of propositional logic, augmented with the
operators  (previously) and
(previously) and
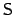 (since),
see e.g., [20]. Whereas a classical propositional logic formula
denotes a set of states (a subset of
(since),
see e.g., [20]. Whereas a classical propositional logic formula
denotes a set of states (a subset of  ), a PLTL formula denotes a
set of finite sequences of states (a subset of
), a PLTL formula denotes a
set of finite sequences of states (a subset of 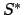 ). A formula
without temporal modality expresses a property that must be true of
the current state, i.e., the last state of the finite sequence.
). A formula
without temporal modality expresses a property that must be true of
the current state, i.e., the last state of the finite sequence.
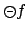 specifies that
specifies that  holds in the previous state (the state
one before the last).
holds in the previous state (the state
one before the last).
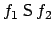 , requires
, requires 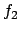 to have been
true at some point in the sequence, and, unless that point is the present,
to have been
true at some point in the sequence, and, unless that point is the present,
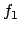 to have held ever since. More formally, the modelling relation
to have held ever since. More formally, the modelling relation
 stating whether a formula
stating whether a formula  holds of a finite sequence
holds of a finite sequence
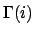 is defined recursively as follows:
is defined recursively as follows:
-
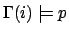 iff
iff  , for
, for  , the set
of atomic propositions
, the set
of atomic propositions
-
 iff
iff

-
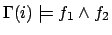 iff
iff
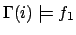 and
and

-
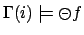 iff
iff 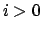 and
and

-
 iff
iff
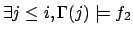 and
and

From
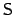 , one can define the useful operators
, one can define the useful operators
![$\makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}f
\equiv \mbox{$\top$}\mathbin{\mbox{\sf S}}f$](img97.png) meaning that
meaning that  has been true at some point,
and
has been true at some point,
and
![$\boxminus f \equiv \neg\makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}\neg f$](img98.png) meaning that
meaning that  has
always been true. E.g,
has
always been true. E.g,
![$g \wedge \neg\circleddash \makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}g$](img99.png) denotes the
set of finite sequences ending in a state where
denotes the
set of finite sequences ending in a state where 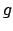 is true for the
first time in the sequence. Other useful abbreviation are
is true for the
first time in the sequence. Other useful abbreviation are
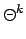 (
(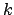 times ago), for
times ago), for 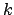 iterations of the
iterations of the  modality,
modality,
![$\makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}_k f$](img102.png) for
for
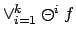 (
( was true at some
of the
was true at some
of the 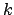 last steps), and
last steps), and
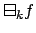 for
for
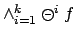 (
( was true at all the
was true at all the 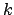 last steps).
Non-Markovian reward functions are described with a set of pairs
last steps).
Non-Markovian reward functions are described with a set of pairs  where
where 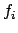 is a PLTL reward formula and
is a PLTL reward formula and 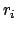 is a real, with
the semantics that the reward assigned to a sequence in
is a real, with
the semantics that the reward assigned to a sequence in 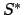 is the
sum of the
is the
sum of the 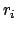 's for which that sequence is a model of
's for which that sequence is a model of 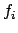 . Below,
we let
. Below,
we let 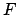 denote the set of reward formulae
denote the set of reward formulae 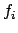 in the description
of the reward function. Bacchus et al. [2] give a list of behaviours which it might be useful to reward, together
with their expression in PLTL. For instance, where
in the description
of the reward function. Bacchus et al. [2] give a list of behaviours which it might be useful to reward, together
with their expression in PLTL. For instance, where  is an
atemporal formula,
is an
atemporal formula,  rewards with
rewards with  units the achievement of
units the achievement of
 whenever it happens. This is a Markovian reward. In contrast
whenever it happens. This is a Markovian reward. In contrast
![$(\makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}f : r)$](img112.png) rewards every state following (and including)
the achievement of
rewards every state following (and including)
the achievement of  , while
, while
![$(f \wedge \neg\circleddash \makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}f: r)$](img113.png) only rewards the first occurrence of
only rewards the first occurrence of  .
.
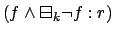 rewards the occurrence of
rewards the occurrence of  at most once every
at most once every 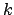 steps.
steps.
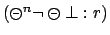 rewards the
rewards the 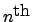 state, independently of its properties.
state, independently of its properties.
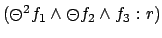 rewards the occurrence of
rewards the occurrence of 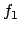 immediately
followed by
immediately
followed by 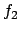 and then
and then 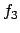 . In reactive planning, so-called
response formulae which describe that the achievement of
. In reactive planning, so-called
response formulae which describe that the achievement of  is
triggered by a condition (or command)
is
triggered by a condition (or command) 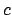 are particularly useful.
These can be written as
are particularly useful.
These can be written as
![$(f \wedge \makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}c: r)$](img120.png) if every state
in which
if every state
in which  is true following the first issue of the command is to be
rewarded. Alternatively, they can be written as
is true following the first issue of the command is to be
rewarded. Alternatively, they can be written as
 if only the first occurrence of
if only the first occurrence of  is to be
rewarded after each command. It is common to only reward the
achievement
is to be
rewarded after each command. It is common to only reward the
achievement  within
within 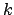 steps of the trigger; we write for example
steps of the trigger; we write for example
![$(f \wedge \makebox[8pt][c]{\makebox[0pt][c]{$\Diamond$}\makebox[0pt][c]{\raisebox{0.5pt}{-}}}_k c : r)$](img122.png) to reward all such states in which
to reward all such states in which
 holds.
From a theoretical point of view, it is known
[38] that the behaviours representable in PLTL
are exactly those corresponding to star-free regular languages. Non
star-free behaviours such as
holds.
From a theoretical point of view, it is known
[38] that the behaviours representable in PLTL
are exactly those corresponding to star-free regular languages. Non
star-free behaviours such as 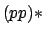 (reward an even number of states
all containing
(reward an even number of states
all containing 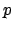 ) are therefore not representable. Nor, of course,
are non-regular behaviours such as
) are therefore not representable. Nor, of course,
are non-regular behaviours such as 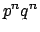 (e.g. reward taking equal
numbers of steps to the left and right). We shall not speculate here
on how severe a restriction this is for the purposes of planning.
Sylvie Thiebaux
2006-01-20
(e.g. reward taking equal
numbers of steps to the left and right). We shall not speculate here
on how severe a restriction this is for the purposes of planning.
Sylvie Thiebaux
2006-01-20