A decision process with non-Markovian rewards is identical to an MDP
except that the domain of the reward function is 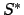 . The idea is
that if the process has passed through state sequence
. The idea is
that if the process has passed through state sequence 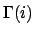 up
to stage
up
to stage 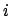 , then the reward
, then the reward 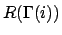 is received at stage
is received at stage
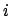 . Figure 1 gives an example. Like the reward
function, a policy for an NMRDP depends on history, and is a mapping
from
. Figure 1 gives an example. Like the reward
function, a policy for an NMRDP depends on history, and is a mapping
from 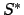 to
to  . As before, the value of policy
. As before, the value of policy 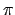 is the
expectation of the discounted cumulative reward over an infinite
horizon:
is the
expectation of the discounted cumulative reward over an infinite
horizon:
For a decision process
 and a state
and a state 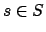 , we let
, we let
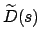 stand for the set of state sequences rooted at
stand for the set of state sequences rooted at
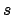 that are feasible under the actions in
that are feasible under the actions in 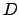 , that is:
, that is:
 . Note that the definition of
. Note that the definition of
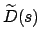 does not depend on
does not depend on 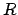 and therefore applies
to both MDPs and NMRDPs.
and therefore applies
to both MDPs and NMRDPs.
Figure 1:
A Simple NMRDP
 |
Sylvie Thiebaux
2006-01-20
![\begin{displaymath}
V_{\pi}(s_{0}) = \lim_{n\rightarrow\infty} \makebox[1em]{$\m...
...} \beta^{i} R(\Gamma(i)) \mid \pi, \Gamma_{0} = s_{0} \bigg{]}
\end{displaymath}](img38.png)