Next: Experimental Setup Up: Application to Artificial Intelligence Previous: Application to Artificial Intelligence
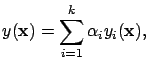 |
(15) |
where ![]() is the output of network
is the output of network ![]() , and
, and
![]() is the weight associated to that network. If the networks have
more than one output, a different weight is usually assigned to each
output. The ensembles of neural networks have some of the advantages
of large networks without their problems of long training time and
risk of over-fitting.
is the weight associated to that network. If the networks have
more than one output, a different weight is usually assigned to each
output. The ensembles of neural networks have some of the advantages
of large networks without their problems of long training time and
risk of over-fitting.
Moreover, this combination of several networks that cooperate in solving a given task has other important advantages, such as [LYH00,Sha96]:
Techniques using multiple models usually consist of two independent phases: model generation and model combination [Mer99b]. Once each network has been trained and assigned a weights (model generation), there are, in a classification environment three basic methods for combining the outputs of the networks (model combination):
The most commonly used methods for combining the networks are the majority voting and sum of the outputs of the networks, both
with a weight vector that measures the confidence in the prediction of
each network. The problem of obtaining the weight vector
![]() is not an easy task. Usually, the values of the
weights
is not an easy task. Usually, the values of the
weights ![]() are constrained:
are constrained:
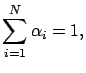 |
(16) |
in order to help to produce estimators with lower prediction error [LT93], although the justification of this constraint is just intuitive [Bre96]. When the method of majority voting is applied, the vote of each network is weighted before it is counted:
 |
(17) |
The problem of finding the optimal weight vector is a very
complex task. The ``Basic ensemble method (BEM)'', as it is called by
Perrone and Cooper [PC93], consists of weighting
all the networks equally.
So, having ![]() networks, the output of the ensembles is:
networks, the output of the ensembles is:
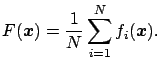 |
(18) |
Perrone and Cooper [PC93] defined the Generalized Ensemble Method, which is equivalent to the Mean Square Error - Optimal Linear Combination (MSE-OLC) without a constant term of Hashem [Has97]. The form of the output of the ensemble is:
where the
![]() are real and satisfy the constraint
are real and satisfy the constraint
![]() . The values of
. The values of ![]() are given by:
are given by:
where ![]() is the symmetric correlation matrix
is the symmetric correlation matrix
![]() , where
, where
![]() defines the misfit of function
defines the misfit of function ![]() , that
is the deviation from the true solution
, that
is the deviation from the true solution
![]() ,
,
![]() .
The previous methods are commonly used. Nevertheless, many other
techniques have been proposed over the last few years. Among others,
there are methods based on linear regression [LT93],
principal components analysis and least-square regression
[Mer99a], correspondence analysis [Mer99b], and the use of
a validation set [OS96].
.
The previous methods are commonly used. Nevertheless, many other
techniques have been proposed over the last few years. Among others,
there are methods based on linear regression [LT93],
principal components analysis and least-square regression
[Mer99a], correspondence analysis [Mer99b], and the use of
a validation set [OS96].
In this application, we use a genetic algorithm for obtaining the weight of each component. This approach is similar to the use of a gradient descent procedure [KW97], avoiding the problem of being trapped in local minima. The use of a genetic algorithm has an additional advantage over the optimal linear combination, as the former is not affected by the collinearity problem [PC93,Has97].