


Next: Lower Bounds on Path Length
Up: Introduction
Previous: Introduction
To begin, we first formalise the concepts of
deal and contract path.
Definition 2
Let
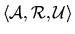
be a resource allocation setting.
A
deal is a pair

where
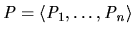
and
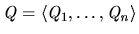
are distinct partitions of

.
The effect of implementing the deal

is that the allocation of resources
specified by
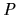
is replaced with that specified by
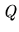
.
Following the notation of
[Endriss & Maudet, 2004b]
for a deal
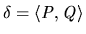
, we use

to indicate the subset of
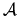
involved, i.e.

if and only if

.
Let
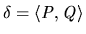 be a deal. A contract path realising
be a deal. A contract path realising 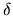 is a sequence of allocations
is a sequence of allocations
in which
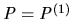
and
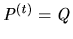
.
The
length of

, denoted

is
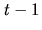
, i.e. the number of
deals in

.
There are two methods which we can use to reduce the number of deals that a single agent may
have to consider in seeking to move from some allocation to another, thereby avoiding the need
to choose from exponentially many alternatives: structural and rationality constraints.
Structural constraints limit the permitted deals to those which bound the number of resources and/or
the number of agents involved, but take no consideration of the view
any agent may have as to whether its allocation has improved. In contrast, rationality constraints
restrict deals
 to those in which
to those in which 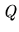 ``improves'' upon
``improves'' upon 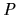 according to particular
criteria. In this article we consider two classes of structural constraint:
according to particular
criteria. In this article we consider two classes of structural constraint: 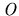 -contracts, defined
and considered in [Sandholm, 1998], and what we shall refer to as
-contracts, defined
and considered in [Sandholm, 1998], and what we shall refer to as  -contracts.
-contracts.
Thus, 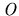 -contracts involve the transfer of exactly one resource from a particular agent
to another, resulting in the number of deals compatible with any given allocation
being exactly
-contracts involve the transfer of exactly one resource from a particular agent
to another, resulting in the number of deals compatible with any given allocation
being exactly  : each of the
: each of the 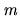 resources can be reassigned from its current owner to any
of the other
resources can be reassigned from its current owner to any
of the other 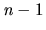 agents.
agents.
Rationality constraints arise in a number of different ways. For example,
from the standpoint of an individual agent  a given deal
a given deal
 may have three different
outcomes:
may have three different
outcomes:
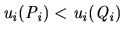 , i.e.
, i.e.
 values the allocation
values the allocation 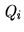 as superior to
as superior to 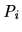 ;
;
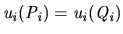 , i.e.
, i.e.  is indifferent between
is indifferent between 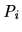 and
and 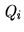 ; and
; and
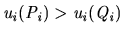 , i.e.
, i.e.  is worse off after the deal.
When global optima such as utilitarian social welfare are to be maximised, there is the question of
what incentive there is for any agent to accept a deal
is worse off after the deal.
When global optima such as utilitarian social welfare are to be maximised, there is the question of
what incentive there is for any agent to accept a deal
 under which it is
left with a less valuable resource holding. The standard approach to this latter question
is to introduce the notion of a pay-off function, i.e.
in order for
under which it is
left with a less valuable resource holding. The standard approach to this latter question
is to introduce the notion of a pay-off function, i.e.
in order for  to accept a deal under which it suffers a reduction in utility,
to accept a deal under which it suffers a reduction in utility,
 receives some payment sufficient to compensate for its loss. Of course such compensation
must be made by other agents in the system who in providing it do not wish to pay
in excess of any gain. In defining notions of pay-off the interpretation
is that in any transaction each agent
receives some payment sufficient to compensate for its loss. Of course such compensation
must be made by other agents in the system who in providing it do not wish to pay
in excess of any gain. In defining notions of pay-off the interpretation
is that in any transaction each agent  makes a payment,
makes a payment,  : if
: if 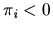 then
then  is given
is given 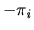 in return for accepting a deal; if
in return for accepting a deal; if 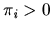 then
then  contributes
contributes  to the amount to be distributed among those agents whose pay-off is negative.
to the amount to be distributed among those agents whose pay-off is negative.
This notion of ``sensible transfer'' is captured by the concept of individual rationality, and
is often defined in terms of an appropriate pay-off vector existing. It is not difficult,
however, to show that such definitions are equivalent to the following.
Definition 4
A deal

is
individually rational (IR) if and only if
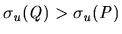
.
We shall consider alternative bases for rationality constraints later: these
are primarily of interest within so-called money free settings
(so that compensatory payment for a loss in utility is not an option).
The central issue of interest in this paper concerns the properties of the contract-net graph
when the allowed deals must satisfy both a structural and a rationality
constraint. Thus, if we consider arbitrary predicates  on deals
on deals
 - where the
cases of interest are
- where the
cases of interest are  combining a structural and rationality condition - we have,
combining a structural and rationality condition - we have,
Definition 5
For

a predicate over distinct pairs of allocations,
a contract path
realising

is a

-
path
if for each

,
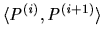
is a

-
deal, that is
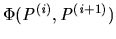
holds.
We say that

is
complete if any deal
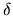
may be realised by a

-path.
We, further, say that

is
complete with respect to 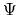
-
deals
(where
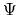
is a predicate over distinct pairs of allocations) if any deal
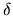
for which
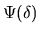
holds may be realised by a

-path.
The main interest in earlier studies of these ideas has been in areas such
as identifying necessary and/or sufficient conditions on deals to be complete with respect to particular
criteria, e.g. [Sandholm, 1998]; and in establishing ``convergence'' and termination
properties, e.g.
[Endriss et al., 2003;
Endriss & Maudet, 2004b] consider deal types,  , such that
every maximal1
, such that
every maximal1  -path
ends in a Pareto optimal allocation, i.e. one in which any reallocation under which
some agent improves its utility will lead to another agent suffering a loss.
Sandholm [1998] examines how restrictions
e.g. with
-path
ends in a Pareto optimal allocation, i.e. one in which any reallocation under which
some agent improves its utility will lead to another agent suffering a loss.
Sandholm [1998] examines how restrictions
e.g. with
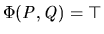 if and only if
if and only if
 is an
is an 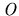 -contract, may affect the existence
of contract paths to realise deals. Of particular interest, from the viewpoint of
heuristics for exploring the contract-net graph, are cases where
-contract, may affect the existence
of contract paths to realise deals. Of particular interest, from the viewpoint of
heuristics for exploring the contract-net graph, are cases where
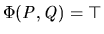 if and only if
the deal
if and only if
the deal
 is individually rational. For the case of
is individually rational. For the case of 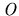 -contracts the following are known:
-contracts the following are known:
Theorem 1

- a.
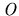 -contracts are complete.
-contracts are complete.
- b.
- IR
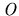 -contracts are not complete with respect to IR deals.
-contracts are not complete with respect to IR deals.
In the consideration of algorithmic and complexity issues
presented in [Dunne et al., 2003]
one difficulty with attempting to formulate reallocation
plans by rational 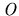 -contracts is already apparent, that is:
-contracts is already apparent, that is:
Theorem 2
Even in the case
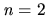
and with monotone utility functions
the problem of deciding if an IR
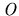
-contract path exists to realise the IR deal

is
NP-hard.
Thus deciding if any rational plan is possible is already computationally hard. In this article
we demonstrate that, even if an appropriate rational plan exists, in extreme cases, there may be
significant problems: the number of deals required could be exponential in the number
of resources, so affecting both the time it will take for the schema outlined to conclude and
the space that an agent will have to dedicate to storing it.
Thus in his proof of Theorem 1 (b), Sandholm observes that when an IR 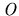 -contract
path exists for a given IR deal, it may be the case that its length exceeds
-contract
path exists for a given IR deal, it may be the case that its length exceeds 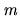 , i.e. some
agent passes a resource to another and then accepts the same resource at a later stage.
, i.e. some
agent passes a resource to another and then accepts the same resource at a later stage.
The typical form of the results that we derive can be summarised as:
For  a structural constraint (
a structural constraint (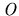 -contract or
-contract or  -contract) and
-contract) and
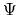 a rationality constraint, e.g.
a rationality constraint, e.g.  holds if
holds if
 is individually rational,
there are resource allocation settings
is individually rational,
there are resource allocation settings
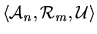 in which
there is a deal
in which
there is a deal
 satisfying all of the following.
satisfying all of the following.
- a.
-
 is a
is a 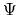 -deal.
-deal.
- b.
-
 can be realised by a contract path on which every deal satisfies the structural
constraint
can be realised by a contract path on which every deal satisfies the structural
constraint  and the rationality constraint
and the rationality constraint 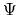 .
.
- c.
- Every such contract path has length at least
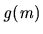 .
.
For example, we show
that there are instances for which the shortest IR  -contract path has length exponential in
-contract path has length exponential in
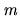 .2In the next section we will be interested in lower bounds on the values of the following functions:
we introduce these in general terms to avoid unnecessary subsequent repetition.
.2In the next section we will be interested in lower bounds on the values of the following functions:
we introduce these in general terms to avoid unnecessary subsequent repetition.
Definition 6
Let
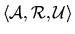
be a resource allocation setting.
Additionally let

and
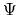
be two predicates on deals. For a deal
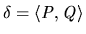
the partial function

is the length of the
shortest 
-contract path realising

if such a
path exists (and is undefined if no such path is possible). The partial function
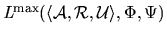
is
Finally, the partial function

is
where consideration is restricted to those
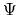
-deals
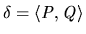
for which a realising

-path exists.
The three measures,  ,
,  and
and  distinguish different aspects
regarding the length of contract-paths. The function
distinguish different aspects
regarding the length of contract-paths. The function  is concerned with
is concerned with  -paths
realising a single deal
-paths
realising a single deal
 in a given resource allocation setting
in a given resource allocation setting
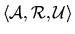 : the
property of interest being the number of deals in the shortest, i.e. optimal length,
: the
property of interest being the number of deals in the shortest, i.e. optimal length,  -path.
We stress that
-path.
We stress that  is a partial function whose value is undefined in the event
that
is a partial function whose value is undefined in the event
that
 cannot be realised by a
cannot be realised by a  -path in the
setting
-path in the
setting
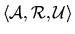 .
The function
.
The function  is defined in terms of
is defined in terms of  , again in the context of a specific
resource allocation setting. The behaviour of interest for
, again in the context of a specific
resource allocation setting. The behaviour of interest for  , however, is not simply the length
of
, however, is not simply the length
of  -paths realising a specific
-paths realising a specific
 but the ``worst-case'' value of
but the ``worst-case'' value of  for
deals which are
for
deals which are 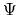 -deals.
We note the qualification that
-deals.
We note the qualification that  is defined only for
is defined only for
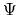 -deals that are capable of being realised by
-deals that are capable of being realised by  -paths,
and thus do not consider cases for which no appropriate
contract path exists. Thus, if it should be the case that no
-paths,
and thus do not consider cases for which no appropriate
contract path exists. Thus, if it should be the case that no 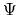 -deal in the setting
-deal in the setting
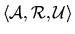 can be realised by a
can be realised by a  -path then
the value
-path then
the value
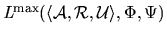 is undefined, i.e.
is undefined, i.e.
 is also a partial function. We may interpret any upper bound on
is also a partial function. We may interpret any upper bound on  in the following terms: if
in the following terms: if
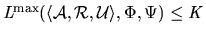 then
any
then
any 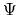 -deal for which a
-deal for which a  -path exists can be realised by a
-path exists can be realised by a  -path of length
at most
-path of length
at most  .
.
Our main interest will centre on  which is concerned with the behaviour
of
which is concerned with the behaviour
of  as a function of
as a function of 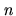 and
and 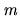 and ranges over all
and ranges over all 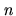 -tuples of utility
functions
-tuples of utility
functions
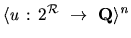 . Our approach to obtaining
lower bounds for this function is constructive, i.e. for each
. Our approach to obtaining
lower bounds for this function is constructive, i.e. for each
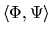 that is
considered, we show how the utility functions
that is
considered, we show how the utility functions 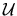 may be defined in a setting with
may be defined in a setting with 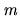 resources
so as to yield a lower bound on
resources
so as to yield a lower bound on
 . In contrast to the measures
. In contrast to the measures
 and
and  , the function
, the function  is not described in terms of a single fixed
resource allocation setting. It is, however, still a partial function: depending on
is not described in terms of a single fixed
resource allocation setting. It is, however, still a partial function: depending on
 it may be the case that in every
it may be the case that in every 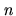 agent,
agent, 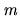 resource allocation setting, regardless of
which choice of utility functions is made, there is no
resource allocation setting, regardless of
which choice of utility functions is made, there is no 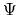 -deal,
-deal,
 capable of
being realised by
capable of
being realised by  -path, and for such cases the value of
-path, and for such cases the value of
 will be undefined.3
will be undefined.3
It is noted, at this point, that the definition of  allows arbitrary
utility functions to be employed in constructing ``worst-case'' instances. While this is reasonable
in terms of general lower bound results, as will be apparent from the given constructions the utility
functions actually employed are highly artificial (and unlikely to feature in ``real'' application settings).
We shall attempt to address this objection by further considering bounds on the following variant of
allows arbitrary
utility functions to be employed in constructing ``worst-case'' instances. While this is reasonable
in terms of general lower bound results, as will be apparent from the given constructions the utility
functions actually employed are highly artificial (and unlikely to feature in ``real'' application settings).
We shall attempt to address this objection by further considering bounds on the following variant of
 :
:

Thus,
 deals with resource allocation settings within which all of the
utility functions must satisfy a monotonicity constraint.
deals with resource allocation settings within which all of the
utility functions must satisfy a monotonicity constraint.
The main results of this article are presented in the next sections. We consider two general
classes of contract path: 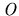 -contract paths under various rationality conditions in
Section 2; and, similarly,
-contract paths under various rationality conditions in
Section 2; and, similarly,
 -contract paths
for arbitrary values of
-contract paths
for arbitrary values of 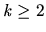 in Section 3.
Our results are concerned with the construction of
resource allocation settings
in Section 3.
Our results are concerned with the construction of
resource allocation settings
 for which given
some rationality requirement, e.g. that deals be individually rational, there is some deal
for which given
some rationality requirement, e.g. that deals be individually rational, there is some deal
 that satisfies the rationality condition, can be realised by a rational
that satisfies the rationality condition, can be realised by a rational 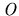 -contract path (respectively,
-contract path (respectively,
 -contract path), but with the number of deals required by such paths being exponential in
-contract path), but with the number of deals required by such paths being exponential in 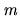 .
We additionally obtain slightly weaker (but still exponential) lower bounds for rational
.
We additionally obtain slightly weaker (but still exponential) lower bounds for rational 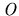 -contract paths
within settings of monotone utility functions, i.e. for the measure
-contract paths
within settings of monotone utility functions, i.e. for the measure
 , outlining how
similar results may be derived for
, outlining how
similar results may be derived for  -contract paths.
-contract paths.
In the resource allocation settings constructed for demonstrating these properties
with  -contract paths, the constructed deal
-contract paths, the constructed deal
 is realisable with
a single
is realisable with
a single  -contract but unrealisable by any rational
-contract but unrealisable by any rational  -contract path.
We discuss related work, in particular the recent study of Endriss-et-al:2004
that addresses similar issues to those considered in the present article, in Section 4.
Conclusions and some directions for further work are presented in the final section.
-contract path.
We discuss related work, in particular the recent study of Endriss-et-al:2004
that addresses similar issues to those considered in the present article, in Section 4.
Conclusions and some directions for further work are presented in the final section.



Next: Lower Bounds on Path Length
Up: Introduction
Previous: Introduction
Paul Dunne
2004-11-26
![]() be a deal. A contract path realising
be a deal. A contract path realising ![]() is a sequence of allocations
is a sequence of allocations
![]() be a deal. A contract path realising
be a deal. A contract path realising ![]() is a sequence of allocations
is a sequence of allocations
![]() a given deal
a given deal
![]() may have three different
outcomes:
may have three different
outcomes:
![]() , i.e.
, i.e.
![]() values the allocation
values the allocation ![]() as superior to
as superior to ![]() ;
;
![]() , i.e.
, i.e. ![]() is indifferent between
is indifferent between ![]() and
and ![]() ; and
; and
![]() , i.e.
, i.e. ![]() is worse off after the deal.
When global optima such as utilitarian social welfare are to be maximised, there is the question of
what incentive there is for any agent to accept a deal
is worse off after the deal.
When global optima such as utilitarian social welfare are to be maximised, there is the question of
what incentive there is for any agent to accept a deal
![]() under which it is
left with a less valuable resource holding. The standard approach to this latter question
is to introduce the notion of a pay-off function, i.e.
in order for
under which it is
left with a less valuable resource holding. The standard approach to this latter question
is to introduce the notion of a pay-off function, i.e.
in order for ![]() to accept a deal under which it suffers a reduction in utility,
to accept a deal under which it suffers a reduction in utility,
![]() receives some payment sufficient to compensate for its loss. Of course such compensation
must be made by other agents in the system who in providing it do not wish to pay
in excess of any gain. In defining notions of pay-off the interpretation
is that in any transaction each agent
receives some payment sufficient to compensate for its loss. Of course such compensation
must be made by other agents in the system who in providing it do not wish to pay
in excess of any gain. In defining notions of pay-off the interpretation
is that in any transaction each agent ![]() makes a payment,
makes a payment, ![]() : if
: if ![]() then
then ![]() is given
is given ![]() in return for accepting a deal; if
in return for accepting a deal; if ![]() then
then ![]() contributes
contributes ![]() to the amount to be distributed among those agents whose pay-off is negative.
to the amount to be distributed among those agents whose pay-off is negative.
![]() on deals
on deals
![]() - where the
cases of interest are
- where the
cases of interest are ![]() combining a structural and rationality condition - we have,
combining a structural and rationality condition - we have,
a structural constraint (
-contract or
-contract) and
a rationality constraint, e.g.
holds if
is individually rational, there are resource allocation settings
in which there is a deal
satisfying all of the following.
![]() which is concerned with the behaviour
of
which is concerned with the behaviour
of ![]() as a function of
as a function of ![]() and
and ![]() and ranges over all
and ranges over all ![]() -tuples of utility
functions
-tuples of utility
functions
![]() . Our approach to obtaining
lower bounds for this function is constructive, i.e. for each
. Our approach to obtaining
lower bounds for this function is constructive, i.e. for each
![]() that is
considered, we show how the utility functions
that is
considered, we show how the utility functions ![]() may be defined in a setting with
may be defined in a setting with ![]() resources
so as to yield a lower bound on
resources
so as to yield a lower bound on
![]() . In contrast to the measures
. In contrast to the measures
![]() and
and ![]() , the function
, the function ![]() is not described in terms of a single fixed
resource allocation setting. It is, however, still a partial function: depending on
is not described in terms of a single fixed
resource allocation setting. It is, however, still a partial function: depending on
![]() it may be the case that in every
it may be the case that in every ![]() agent,
agent, ![]() resource allocation setting, regardless of
which choice of utility functions is made, there is no
resource allocation setting, regardless of
which choice of utility functions is made, there is no ![]() -deal,
-deal,
![]() capable of
being realised by
capable of
being realised by ![]() -path, and for such cases the value of
-path, and for such cases the value of
![]() will be undefined.3
will be undefined.3
![]() allows arbitrary
utility functions to be employed in constructing ``worst-case'' instances. While this is reasonable
in terms of general lower bound results, as will be apparent from the given constructions the utility
functions actually employed are highly artificial (and unlikely to feature in ``real'' application settings).
We shall attempt to address this objection by further considering bounds on the following variant of
allows arbitrary
utility functions to be employed in constructing ``worst-case'' instances. While this is reasonable
in terms of general lower bound results, as will be apparent from the given constructions the utility
functions actually employed are highly artificial (and unlikely to feature in ``real'' application settings).
We shall attempt to address this objection by further considering bounds on the following variant of
![]() :
:
![]() -contract paths under various rationality conditions in
Section 2; and, similarly,
-contract paths under various rationality conditions in
Section 2; and, similarly,
![]() -contract paths
for arbitrary values of
-contract paths
for arbitrary values of ![]() in Section 3.
Our results are concerned with the construction of
resource allocation settings
in Section 3.
Our results are concerned with the construction of
resource allocation settings
![]() for which given
some rationality requirement, e.g. that deals be individually rational, there is some deal
for which given
some rationality requirement, e.g. that deals be individually rational, there is some deal
![]() that satisfies the rationality condition, can be realised by a rational
that satisfies the rationality condition, can be realised by a rational ![]() -contract path (respectively,
-contract path (respectively,
![]() -contract path), but with the number of deals required by such paths being exponential in
-contract path), but with the number of deals required by such paths being exponential in ![]() .
We additionally obtain slightly weaker (but still exponential) lower bounds for rational
.
We additionally obtain slightly weaker (but still exponential) lower bounds for rational ![]() -contract paths
within settings of monotone utility functions, i.e. for the measure
-contract paths
within settings of monotone utility functions, i.e. for the measure
![]() , outlining how
similar results may be derived for
, outlining how
similar results may be derived for ![]() -contract paths.
-contract paths.
![]() -contract paths, the constructed deal
-contract paths, the constructed deal
![]() is realisable with
a single
is realisable with
a single ![]() -contract but unrealisable by any rational
-contract but unrealisable by any rational ![]() -contract path.
We discuss related work, in particular the recent study of Endriss-et-al:2004
that addresses similar issues to those considered in the present article, in Section 4.
Conclusions and some directions for further work are presented in the final section.
-contract path.
We discuss related work, in particular the recent study of Endriss-et-al:2004
that addresses similar issues to those considered in the present article, in Section 4.
Conclusions and some directions for further work are presented in the final section.