Next: Study of cycles Up: Global approach (with tuples) Previous: Global approach (with tuples)
First, in order to record the lengths of the branches leading to the arguments, we use the notion of tuples and we define some operations on these tuples:
 will be denoted by
will be denoted by  will be
denoted by
will be
denoted by
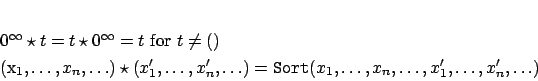

Note that we allow infinite tuples, among other reasons, because they are needed later in order to compute the ordering relations described in Section 3.2.4 (in particular when the graph is cyclic).
The operations on the tuples have the following properties:
For any tuple ![]() and any integers
and any integers ![]() and
and ![]() ,
,
![]() .
.
For any integer ![]() and any tuples
and any tuples ![]() and
and ![]() different from
different from
![]() 17,
17,
![]() .
.
In order to valuate the arguments, we split the set of the lengths of the branches leading to the argument in two subsets, one for the lengths of defence branches (even integers) and the other one for the lengths of attack branches (odd integers). This is captured by the notion of tupled values:
Using this notion of tupled-values, we can define the computation process of the gradual valuation with tuples18 in the case of acyclic graphs.
Ifis a leaf then
.
Ifhas direct attackers denoted by
, ...,
, ...then
with:
|
|
Notes: The choice of the value
![]() for the leaves
is justified by the fact that the value of an argument memorises all
the lengths of the branches leading to the argument. Using the same
constraint, either
for the leaves
is justified by the fact that the value of an argument memorises all
the lengths of the branches leading to the argument. Using the same
constraint, either ![]() or
or ![]() may be empty but not
both19.
may be empty but not
both19.
Note also that the set of the direct attackers of an argument can be infinite (this property will be used when we take into account an argumentation graph with cycles).
|
|
Marie-Christine Lagasquie 2005-02-04