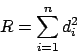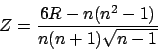Spearman's Rank Correlation Test

This is a test for correlation between a sequence of pairs of values. Using ranks eliminates the sensitivity of the correlation test to the function linking the pairs of values. In particular, the standard correlation test is used to find linear relations between test pairs, but the rank correlation test is not restricted in this way.

Given $n$ pairs of observations, $(x_i,y_i)$, the $x_i$ values are assigned a rank value and, separately, the $y_i$ values are assigned a rank. For each pair $(x_i,y_i)$, the corresponding difference, $d_i$ between the $x_i$ and $y_i$ ranks is found. The value $R$ is:

$$R = \sum^n_{i=1} d_{i}^2$$

For large samples the test statistic is then:

$$Z = \frac{6R - n(n^2-1)}{n(n+1)\sqrt{n-1}}$$

which is approximately normally distributed.