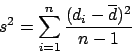The t-test

The t-test is a parametric test: it is founded on an assumption that the underlying population from which the samples are drawn is nearly normally distributed. It is reasonably robust to failures in this assumption, but should be treated with caution as the true distribution deviates from normal. The test considers means of two samples and tests the null hypothesis that the two samples are drawn from populations with the same mean. Variants are available according to what is known about variance in the underlying populations. The t-test is a more conservative version of the Z-test, which relies on the effect confirmed by the Central Limit Theorem that, for large samples, the sampling ditribution of the mean is normal. The t-test can be applied with smaller samples, compensating for the distortion of the distribution that this creates. In this paper, we use a variant of the t-test in which observations are drawn in matched pairs: each element of a pair is a test result conducted under close to identical circumstances, but for a different test subject (in this case, a different planner).

For $n$ pairs of observations, where $d_i$ is the difference for pair $i$ and $\overline{d}$ is the mean difference, the variance, $s$, of the differences is given by:

$$s^2 = \sum^{n}_{i=1} \frac{(d_i - \overline{d})^2}{n-1}$$

If $\overline{x_1}$ and $\overline{x_2}$ are the means of the samples from each of the two populations, then the statistic is:

$$t = \frac{\overline{x_1} - \overline{x_2}}{s/\sqrt{n}}$$

with $n-1$ degrees of freedom.