


Next: TAC
Up: General Approach
Previous: The Full Approach
Consider a camera and a flash with interacting values to an agent as
shown in Table 2. Further, consider that the agent
estimates that the camera will sell for $40 with probability 25%,
$70 with probability 50%, and $95 with probability 25%. Consider the
question of what the agent should bid for the flash (in auction
 ). The decision pertaining to the camera would be made via a
similar analysis.
). The decision pertaining to the camera would be made via a
similar analysis.
Table 2:
The table of values for all combination of camera and flash
in our example.
| |
utility |
| camera alone |
$50 |
| flash alone |
10 |
| both |
100 |
| neither |
0 |
|
First, the agent samples from the distribution of possible camera
prices. When the price of the camera (sold in auction  ) is $70
in the sample:
) is $70
in the sample:
-

-
 is the best set of purchases the agent
can make with the flash, and assuming the camera costs $70. In this
case, the only two options are buying the camera or not. Buying the
camera yields a profit of
is the best set of purchases the agent
can make with the flash, and assuming the camera costs $70. In this
case, the only two options are buying the camera or not. Buying the
camera yields a profit of  . Not buying the
camera yields a profit of
. Not buying the
camera yields a profit of 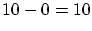 . Thus,
. Thus,  , and
, and
![$[v(G_w+H) - G_w \cdot Y] = v(1,1) - (0,1) \cdot (\infty,70) = 100 - 70$](img72.png) .
.
- Similarly
 (since if the flash is not owned, buying
the camera yields a profit of
(since if the flash is not owned, buying
the camera yields a profit of  , and not buying it
yields a profit of
, and not buying it
yields a profit of  ) and
) and
![$[v(G+H) - G \cdot Y] = 0$](img76.png) .
.
-
 .
.
Similarly, when the camera is predicted to cost $40,
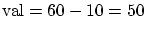 ; and when the camera is predicted to cost
$95,
; and when the camera is predicted to cost
$95,
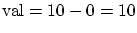 . Thus, we expect that 50% of the
camera price samples will suggest a flash value of $30, while 25%
will lead to a value of $50 and the other 25% will lead to a value
of $10. Thus, the agent will bid
. Thus, we expect that 50% of the
camera price samples will suggest a flash value of $30, while 25%
will lead to a value of $50 and the other 25% will lead to a value
of $10. Thus, the agent will bid
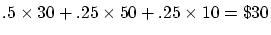 for the flash.
for the flash.
Notice that in this analysis of what to bid for the flash, the actual
closing price of the flash is irrelevant. The proper bid depends only
on the predicted price of the camera. To determine the proper bid for
the camera, a similar analysis would be done using the predicted price
distribution of the flash.



Next: TAC
Up: General Approach
Previous: The Full Approach
Peter Stone
2003-09-24
![]() ). The decision pertaining to the camera would be made via a
similar analysis.
). The decision pertaining to the camera would be made via a
similar analysis.
![]() ) is $70
in the sample:
) is $70
in the sample: