 |
 |
It is possible to derive the fixed point of the bound propagation
algorithm analytically for a Boltzmann ring if we take a single value
for all weights (![]() ) and one for all thresholds (
) and one for all thresholds (![]() ). Due to this
symmetry all single node marginals are equal in such a network. Moreover
all upper and lower bounds on the single nodes should be identical.
This implies that for the fixed point the following holds for any
). Due to this
symmetry all single node marginals are equal in such a network. Moreover
all upper and lower bounds on the single nodes should be identical.
This implies that for the fixed point the following holds for any ![]() :
:
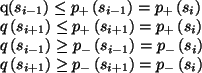
![[*]](crossref.png) is given by
is given by
| (13) |
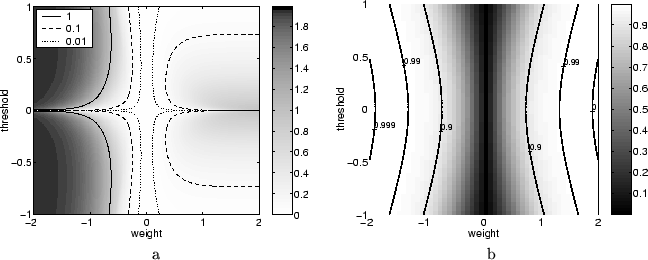
In Figure ![[*]](crossref.png) a the difference between the upper and
lower bound on the means is shown for various choices of the weight
and threshold. As we saw before tight bounds can be obtained for
small weights and somewhat larger, but positive weights, whereas
negative weights result in rather poor, but still non-trivial bounds.
It should be mentioned, however, that these results correspond to
the choice of the smallest clusters (
a the difference between the upper and
lower bound on the means is shown for various choices of the weight
and threshold. As we saw before tight bounds can be obtained for
small weights and somewhat larger, but positive weights, whereas
negative weights result in rather poor, but still non-trivial bounds.
It should be mentioned, however, that these results correspond to
the choice of the smallest clusters (
![]() and
and
![]() ) for the bound propagation algorithm.
The bounds can easily be improved by enlarging the clusters as we saw
in Figure
) for the bound propagation algorithm.
The bounds can easily be improved by enlarging the clusters as we saw
in Figure ![[*]](crossref.png) .
.
Close to the fixed point the bound propagation algorithm converges
exponentially. The distance to the asymptotic value can be written
as ![]() , where
, where ![]() is the number of iterations and
is the number of iterations and ![]() is a number between zero and one indicating the convergence speed.
The closer to one
is a number between zero and one indicating the convergence speed.
The closer to one ![]() is, the slower the algorithm converges.
In Figure
is, the slower the algorithm converges.
In Figure ![[*]](crossref.png) b
b ![]() is shown for the same weights and
thresholds. It is clear that larger weights induce a slower convergence.
That is what we see in general: probabilities that are close to
deterministic slow down the convergence.
is shown for the same weights and
thresholds. It is clear that larger weights induce a slower convergence.
That is what we see in general: probabilities that are close to
deterministic slow down the convergence.