Next: Fixed Points and Convergence Up: Bound Propagation Previous: Computational Complexity

A Toy Problem

**Figure:** A Boltzmann machine ring of 200 nodes is initialized with thresholds and weights as shown in the lower part of the figure. Exact means are plotted as well as the results of the bound propagation algorithm. The number of nodes included in $S_\mathrm{\scriptscriptstyle mar}$ is indicated in the legend.
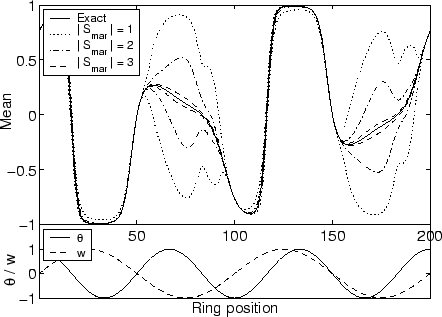
$\begin{figure}{\centering\epsfig{file=ringtest.eps,width=10cm}\par\par } \end{figure}$

To get some intuition about the performance of the algorithm we created a ring (one large loop) of 200 binary nodes. Nodes are connected as in the Boltzmann machine with a weight and each node has a threshold $\theta$ . Weights and thresholds are varying along the ring as is shown at the bottom of Figure . For this simple problem we can compute the exact single node marginals. These are plotted as a solid line in Figure . We ran the bound propagation algorithm three times, where we varied the maximum number of nodes included in $S_\mathrm{\scriptscriptstyle mar}$ : $\left\vert S_\mathrm{\scriptscriptstyle mar}\right\vert=1$ , $\left\vert S_\mathrm{\scriptscriptstyle mar}\right\vert=2$ and $\left\vert S_\mathrm{\scriptscriptstyle mar}\right\vert=3$ . In all cases we chose two separator nodes: the two neighbors of $S_\mathrm{\scriptscriptstyle mar}$ . Thus these three cases correspond to $\Omega\left(2^3\right)$ , $\Omega\left(2^4\right)$ and $\Omega\left(2^5\right)$ . As is clear from Figure the simplest choice already find excellent bounds for the majority of the nodes. For large negative weights, however, this choice is not sufficient. Allowing larger separators clearly improves the result. In all cases the computation time was a few seconds².

Subsections

Fixed Points and Convergence

Next: Fixed Points and Convergence Up: Bound Propagation Previous: Computational Complexity

Martijn Leisink 2003-08-18