

Next: A Simple Example
Up: What Bounds Can Learn
Previous: What Bounds Can Learn
Figure:
The area in which
 must lie is shown.
must lie is shown.
 is implicitly given since the distribution is normalized.
a) The pyramid is the allowable space. The darker planes show how
this pyramid can be restricted by adding earlier computed bounds as
constraints in the linear programming problem. b) This results in a
smaller polyhedron. The black lines show the planes where the
function
is implicitly given since the distribution is normalized.
a) The pyramid is the allowable space. The darker planes show how
this pyramid can be restricted by adding earlier computed bounds as
constraints in the linear programming problem. b) This results in a
smaller polyhedron. The black lines show the planes where the
function
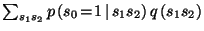 is
constant for this particular problem.
is
constant for this particular problem.
 |
In terms of standard linear programming, Equation ![[*]](crossref.png) can be
expressed as
can be
expressed as
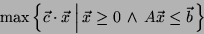 |
(7) |
where the variables are defined as

where
![$\delta\left({\vec s\makebox[0pt][l]{$ '$}}_\mathrm{\scriptscriptstyle mar},\vec s_\mathrm{\scriptscriptstyle sep}\right)=1$](img34.png) iff the states of the
nodes both node sets have in common are equal. Thus the columns of
the matrix
iff the states of the
nodes both node sets have in common are equal. Thus the columns of
the matrix 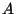 correspond to
correspond to
 , the rows of
, the rows of 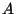 and
and  to
all the constraints (of which we have
to
all the constraints (of which we have
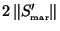 for each
for each
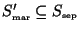 ). The ordering of the rows of
). The ordering of the rows of 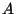 and
and  is irrelevant as long as it is the same for both. The constraint
that
is irrelevant as long as it is the same for both. The constraint
that
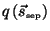 should be normalized can be incorporated in
should be normalized can be incorporated in  and
and  by requiring
by requiring
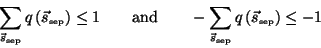 |
(8) |
The maximum of
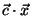 corresponds to
corresponds to
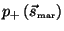 .
The negative of
.
The negative of
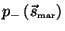 can be found by using
can be found by using
 as the objective function.
as the objective function.


Next: A Simple Example
Up: What Bounds Can Learn
Previous: What Bounds Can Learn
Martijn Leisink
2003-08-18


![[*]](crossref.png) can be
expressed as
can be
expressed as
