

Next: Bibliography
Up: Bound Propagation
Previous: The Bi-Partite Graph
Discussion
We have shown that bound propagation is a simple algorithm with
surprisingly good results. It performs exact computations on local parts
of the network and keeps track of the uncertainties that brings along.
In this way it is capable to compute upper and lower bounds on any
marginal probability of a small set of nodes in the intractable network.
Currently we do not understand which network properties are responsible
for the tightness of the bounds found. In Figure ![[*]](crossref.png) , for
instance, we saw islands of worse results in a sea of tight bounds.
It is obvious that one bad bound influences its direct neighbourhood,
since bound propagation performs local computations in the network.
We have no clue, however, why these islands are at the location we
found them. We tried to find a correlation with the size of the weights
(rewriting the network potentials to a Boltzmann distribution) or with
the local frustration of the network (spin glass state), but could
not explain the quality of the bounds in terms of these quantities.
Here we pose it as an open question.
, for
instance, we saw islands of worse results in a sea of tight bounds.
It is obvious that one bad bound influences its direct neighbourhood,
since bound propagation performs local computations in the network.
We have no clue, however, why these islands are at the location we
found them. We tried to find a correlation with the size of the weights
(rewriting the network potentials to a Boltzmann distribution) or with
the local frustration of the network (spin glass state), but could
not explain the quality of the bounds in terms of these quantities.
Here we pose it as an open question.
The computational complexity of the algorithm is mainly determined by the
state space of the separator nodes one uses, which makes the algorithm
unsuitable for heavily connected networks such as Boltzmann machines.
Nevertheless, there is a large range of architectures for which bound
propagation can easily be done. Such networks typically have a limited
number of connections per node which makes the majority of the Markov
blankets small enough to be tractable for the bound propagation algorithm.
We want to discuss one important property of the bound propagation
algorithm we did not address before. In this article we found
our set of
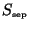 's by Equation
's by Equation ![[*]](crossref.png) . Due to this
choice the separator nodes will always be in the neighbourhood of
. Due to this
choice the separator nodes will always be in the neighbourhood of
 . We have, however, much more freedom to choose
. We have, however, much more freedom to choose
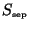 .
In Section
.
In Section ![[*]](crossref.png) we stated that a sufficient condition to make the
algorithm tractable is that
we stated that a sufficient condition to make the
algorithm tractable is that
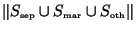 is small enough to do exact computations. A more general, but still
sufficient condition is that we should choose
is small enough to do exact computations. A more general, but still
sufficient condition is that we should choose
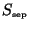 such that
such that
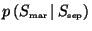 can be computed efficiently, since
this is the quantity we need (see Equation
can be computed efficiently, since
this is the quantity we need (see Equation ![[*]](crossref.png) ). If the network
structure inside the area separated by
). If the network
structure inside the area separated by
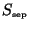 can be written as
a junction tree with a small enough tree width, we can compute these
conditional probabilities even if the number of nodes enclosed by
can be written as
a junction tree with a small enough tree width, we can compute these
conditional probabilities even if the number of nodes enclosed by
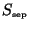 is very large. For certain architectures the separator
can even in that case be small enough. One can think of a network
consisting of a number of tractable junction trees that are connected
to each other by a small number of nodes. One should be aware of the
important difference between the method outlined here and the method
of conditioning pearl88a, which does exact inference.
We do not require the part of the network that is outside the separator
(i.e. all nodes not in
is very large. For certain architectures the separator
can even in that case be small enough. One can think of a network
consisting of a number of tractable junction trees that are connected
to each other by a small number of nodes. One should be aware of the
important difference between the method outlined here and the method
of conditioning pearl88a, which does exact inference.
We do not require the part of the network that is outside the separator
(i.e. all nodes not in
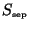 ,
,
 or
or
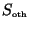 ) to
be tractable. The open problem is to develop an efficient algorithm
to find suitable separators, since the nodes in such an
) to
be tractable. The open problem is to develop an efficient algorithm
to find suitable separators, since the nodes in such an
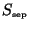 are generally spread widely.
are generally spread widely.
To conclude this article we like to say a few more words about linear
programming. This is a field of research that is still developing.
Any improvements on LP-solving algorithms directly
influence the results presented in this article. We could imagine
that more advanced LP-methods could benefit from the fact that
the matrix 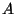 in Equation
in Equation ![[*]](crossref.png) is sparse. At least half of the
entries are zero. To be more precise: the constraints induced by a
particular
is sparse. At least half of the
entries are zero. To be more precise: the constraints induced by a
particular
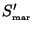 are exactly
are exactly
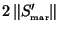 rows
in the matrix
rows
in the matrix 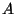 with exactly
with exactly
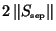 non-zero entries,
thus having a fraction of
non-zero entries,
thus having a fraction of
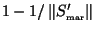 zero´s. Moreover,
all the non-zero entries are ones. Finally, there is a promising future
for LP-solvers, since the algorithms seems to be suitable for
parallel computing alon90parallel.
zero´s. Moreover,
all the non-zero entries are ones. Finally, there is a promising future
for LP-solvers, since the algorithms seems to be suitable for
parallel computing alon90parallel.
This research is supported by the Technology Foundation
STW, applied science devision of NWO and the
technology programme of the Ministry of Economic Affairs.


Next: Bibliography
Up: Bound Propagation
Previous: The Bi-Partite Graph
Martijn Leisink
2003-08-18
![[*]](crossref.png) , for
instance, we saw islands of worse results in a sea of tight bounds.
It is obvious that one bad bound influences its direct neighbourhood,
since bound propagation performs local computations in the network.
We have no clue, however, why these islands are at the location we
found them. We tried to find a correlation with the size of the weights
(rewriting the network potentials to a Boltzmann distribution) or with
the local frustration of the network (spin glass state), but could
not explain the quality of the bounds in terms of these quantities.
Here we pose it as an open question.
, for
instance, we saw islands of worse results in a sea of tight bounds.
It is obvious that one bad bound influences its direct neighbourhood,
since bound propagation performs local computations in the network.
We have no clue, however, why these islands are at the location we
found them. We tried to find a correlation with the size of the weights
(rewriting the network potentials to a Boltzmann distribution) or with
the local frustration of the network (spin glass state), but could
not explain the quality of the bounds in terms of these quantities.
Here we pose it as an open question.