


Next: Proof of Lemma 1
Up: Appendix A
Previous: Proof of Theorem 4
The reduction is made from the 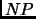 -Hard problem 3SAT5 [Feige1996]. This is the classical 3SAT problem [Garey Johnson1979], but each variable appears in exactly 5 clauses. Using a well-known reduction [Garey Johnson1979], page 55, with an additional simple gadget, we can make a reduction from 3SAT5 to vertex cover (thus, independent set), obtaining a graph
-Hard problem 3SAT5 [Feige1996]. This is the classical 3SAT problem [Garey Johnson1979], but each variable appears in exactly 5 clauses. Using a well-known reduction [Garey Johnson1979], page 55, with an additional simple gadget, we can make a reduction from 3SAT5 to vertex cover (thus, independent set), obtaining a graph  in which all vertices have degree either 5, or 0, and for which the largest independent set (for satisfiable instances of 3SAT5) has size
in which all vertices have degree either 5, or 0, and for which the largest independent set (for satisfiable instances of 3SAT5) has size 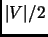 , where
, where  is the number of vertices of
is the number of vertices of  . From this particular graph, we build a simple reduction to our problem of maximizing
. From this particular graph, we build a simple reduction to our problem of maximizing 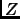 . Note that since we are searching for an oblivious hypothesis, the observations are not important (we can suppose that all examples have the same observation). That is why the reduction only builds class vectors (over
. Note that since we are searching for an oblivious hypothesis, the observations are not important (we can suppose that all examples have the same observation). That is why the reduction only builds class vectors (over  classes), encoding the class membership of any of these identical observations. The idea is that the classes are in one-to-one mapping with the vertices, and there are two sets of class vectors built from
classes), encoding the class membership of any of these identical observations. The idea is that the classes are in one-to-one mapping with the vertices, and there are two sets of class vectors built from  :
:
- a set with
 vectors, encoding the vertices of
vectors, encoding the vertices of  . Each one is a class vector with only one ``1'' corresponding to the vertex, and the remaining components are zeroes. Each of the corresponding examples have weight
. Each one is a class vector with only one ``1'' corresponding to the vertex, and the remaining components are zeroes. Each of the corresponding examples have weight  .
.
- a set with
 vectors, where
vectors, where  is the number of edges of
is the number of edges of  . Each one encodes an edge, and therefore contains two ``1'' (and the remaining are zeroes) corresponding to the two vertices of the edge. Each of the corresponding examples have weight
. Each one encodes an edge, and therefore contains two ``1'' (and the remaining are zeroes) corresponding to the two vertices of the edge. Each of the corresponding examples have weight  .
.
Consider formulas (2), (3) for example. They are the sum of the contribution to 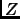 of the examples having weight
of the examples having weight  , and the examples having weight
, and the examples having weight  . In these cases, we can rewrite
. In these cases, we can rewrite 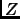 using the generic expression:
using the generic expression:
Here, 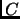 is the number of edges having their two vertices in the set corresponding to the
is the number of edges having their two vertices in the set corresponding to the 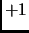 values in
values in 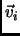 ,
,  is the number of edges having their two vertices in the set corresponding to the
is the number of edges having their two vertices in the set corresponding to the 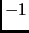 values in
values in 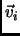 , and
, and 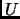 is the number of edges having one of their vertices in the
is the number of edges having one of their vertices in the 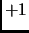 set, and the other one in the
set, and the other one in the 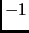 set.
set. 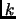 is the number of
is the number of 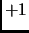 values in
values in 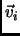 .
.
Suppose that  (e.g.
(e.g.
 ). Then the maximization of
). Then the maximization of 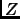 is the maximization of
is the maximization of 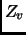 , followed by the maximization of
, followed by the maximization of  .
. 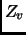 admits a maximum for
admits a maximum for  , and with this value for
, and with this value for 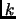 , it can be shown that maximizing
, it can be shown that maximizing  boils down to maximize
boils down to maximize  , that is, the (weighted) number of edges not falling entirely into the set corresponding to the
, that is, the (weighted) number of edges not falling entirely into the set corresponding to the 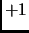 values; whenever the 3SAT5 instance is satisfiable (and using the particular degrees of the vertices), this set corresponds to the largest independent set of
values; whenever the 3SAT5 instance is satisfiable (and using the particular degrees of the vertices), this set corresponds to the largest independent set of  .
.



Next: Proof of Lemma 1
Up: Appendix A
Previous: Proof of Theorem 4
©2002 AI Access Foundation and Morgan Kaufmann Publishers. All rights reserved.
![]() -Hard problem 3SAT5 [Feige1996]. This is the classical 3SAT problem [Garey Johnson1979], but each variable appears in exactly 5 clauses. Using a well-known reduction [Garey Johnson1979], page 55, with an additional simple gadget, we can make a reduction from 3SAT5 to vertex cover (thus, independent set), obtaining a graph
-Hard problem 3SAT5 [Feige1996]. This is the classical 3SAT problem [Garey Johnson1979], but each variable appears in exactly 5 clauses. Using a well-known reduction [Garey Johnson1979], page 55, with an additional simple gadget, we can make a reduction from 3SAT5 to vertex cover (thus, independent set), obtaining a graph ![]() in which all vertices have degree either 5, or 0, and for which the largest independent set (for satisfiable instances of 3SAT5) has size
in which all vertices have degree either 5, or 0, and for which the largest independent set (for satisfiable instances of 3SAT5) has size ![]() , where
, where ![]() is the number of vertices of
is the number of vertices of ![]() . From this particular graph, we build a simple reduction to our problem of maximizing
. From this particular graph, we build a simple reduction to our problem of maximizing ![]() . Note that since we are searching for an oblivious hypothesis, the observations are not important (we can suppose that all examples have the same observation). That is why the reduction only builds class vectors (over
. Note that since we are searching for an oblivious hypothesis, the observations are not important (we can suppose that all examples have the same observation). That is why the reduction only builds class vectors (over ![]() classes), encoding the class membership of any of these identical observations. The idea is that the classes are in one-to-one mapping with the vertices, and there are two sets of class vectors built from
classes), encoding the class membership of any of these identical observations. The idea is that the classes are in one-to-one mapping with the vertices, and there are two sets of class vectors built from ![]() :
: