The speed up obtained using function composition is sufficiently large that small variations in the experimental set up should be unlikely to affect the overall result. Nevertheless, there are a number of concerns that might be raised about the experimental methodology. Some will be, at least partially, addressed in this section; others will be the subject of future work.
The first concern might be how the estimated value of speed up is measured. The value represents the speed up of the average of a set of learning tasks, rather than the average of the speed up in each of the tasks. One of the difficulties of estimation, with curves for single tasks, is that the average distance to goal may oscillate up and down as learning progresses, even though the general trend is downwards. This makes judging the position of the knee of the curves difficult, and any estimate of speed up questionable. Even experimental runs using the same configuration, but with different random seeds, exhibit a considerable variation. In some instances, the speed up measured on individual curves may benefit the function composition system, in others, the baseline algorithm. Nevertheless, probably overall most of these effects will cancel out.
The second concern might be the effect on speed up of the limit of 2000 steps when measuring the distance to the goal. Comparing two averages of values limited in this way is sometimes misleading (Gordon & Segre 1996). But this limit primarily affects only the baseline algorithm, and was only significant when the goal was moved and the function not reinitialized. Estimation of speed up is principally concerned with comparing the position of the knees of the different curves. Here, the average distance to goal is relatively small, so limiting the value is likely to have little effect.
The third concern might be that the value of speed up is dependent on
the configuration of the baseline algorithm. Certainly, it is the
experience of this author that the way the function is initialized,
and how actions are selected, can have an impact on the speed of
learning. In previous work (Drummond 1998), the function was
initialized to a constant value of 0.75, a technique termed ``optimistic
initial values'' by Sutton and Barto (1998). Tie breaking
between actions of the same value was achieved by adding a small
amount of noise (circa 
). It was expected that
this would increase exploration early on in the learning process and
speed up learning overall. However, using an initial value of zero
and a strict tie-breaker, randomly selecting amongst actions with the
same value, turned out to produce a significant speed up in the
baseline learning algorithm. This configuration was used for the
preceding experiments, but on one experimental run this caused serious
problems for the baseline algorithm.
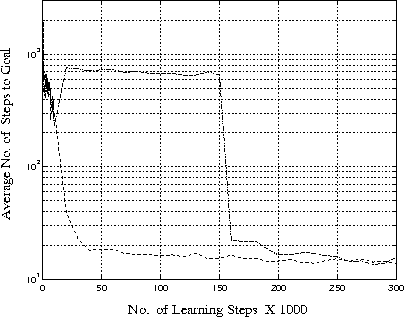
The upper learning curve of Figure 34 is for the baseline algorithm, for one run when the goal was moved in the robot arm domain. As it had such a large impact on the average learning curve, it was replaced by the lower curve, produced by repeating the experiment with a different random seed. This very slow learning rate arises from the interaction of the partial observability of the robot arm domain with the use of an initial value of zero. Individual cells of the function approximator straddle the obstacles allowing a ``leak-through'' of value from one side of the obstacle to the other. Starting with a zero value, once an action receives some value it will remain the best action for some time. Continual update of this action will decrease the value, but it can only asymptotically approach zero. Until other actions for the same state are updated, it will always be selected as the greedy action. This did not occur for higher initial values. It may be that in domains where there is some degree of partial observability, small initial values are better than zero or some means of improving exploration for very small values might be necessary.
Other variations in the parameters of the baseline algorithm have not
been explored in this paper. For instance, a constant learning rate of
0.1 was used. Alternatives, such as starting with a higher rate and
reducing it as learning progresses might also improve the overall
speed of the baseline algorithm. Some preliminary experiments were,
however, carried out using undiscounted reinforcement learning, the
discounting being strictly unnecessary in goal-directed tasks. Room
configuration 1 of Figure 26, with the goal in the lower
right hand corner, was used as the experimental task. The
discounting, discussed in Section 3.1, is turned off by
setting 
to 1. In addition, the value on reaching the goal
state is set to zero and a cost is associated with every action. This
form of learning simplifies function composition, normalization
procedures needed to compensate for the value function's exponential
form being no longer required. With normalization disabled, the snake
successfully partitioned the function, the most critical part of the
process. However, the baseline learner took considerably longer to
learn the function than in the discounted case. With discounting, the
learner reached an average distance to goal of about 72 steps after
80,000 learning steps. Without discounting, the learner reached an
average of 400 steps at the same point in time and only an average of
80 steps after 300,000 learning steps. The action-value function was
initialized to zero, which appears to be the standard practice in the
literature. However, the experience with initialization in the
discounted case suggests this might be the part of problem and this
will be investigated in future work.
The baseline Q-learning algorithm used is the most basic and a more sophisticated one would unquestionably reduce the speed up experimentally obtained. For instance, some form of reinforcement learning using eligibility traces (Singh & Sutton 1996) might be used. For the experiments when the goal was moved, a baseline such Dyna-Q+ (Sutton 1990) which was specifically designed to deal with changing worlds would probably be a better reference point.
The speed up obtained, by transferring pieces of an action-value function, has also not been compared to alternatives, such as transferring pieces of a policy or transferring pieces of a model. Transferring pieces of a policy would reduce memory requirements and not require the rescaling applied to pieces of an action-value function. It does, however, have two disadvantages. Firstly, a solution can not be directly composed, as the position of decision boundaries can not be determined. Further learning would be necessary to decide the appropriate policy for each room. Secondly, the policy only indicates the best action. The action-value function orders the actions, indicating potentially useful small changes to the policy which might improve the accuracy on a new task. Transferring pieces of a model, would require first learning a model consisting of a probability distribution function for each action in each state. The memory requirement is considerably larger, unless the states reachable by an action are limited beforehand. Nevertheless, a model would need less modification in a changing world, such as when the goal is moved. It also carries more information which might speed up learning. The action-value function seems a good compromise in terms of complexity versus information content, but this would need to be empirically validated and is the subject of future work.