

Next: Other Algorithms Based on
Up: Refinement of a Single
Previous: Refinement of a Single
The first algorithm we discuss is TILDE [5], an
algorithm that builds first-order decision trees. In a first-order
decision tree, nodes contain literals that together with the
conjunction of the literals in the nodes above this node (i.e., in a
path from the root to this node) form the query that is to be run for
an example to decide which subtree it should be sorted into. When
building the tree, the literal (or conjunction of literals) to be
put in one node is chosen as
follows: given the query corresponding to a path from the root to this
node, generate all refinements of this query (a refinement of a query
is formed by adding one or more literals to the query); evaluate these
refinements on the relevant subset of the data,2 computing, e.g., the information gain
[25] yielded by the refinement; choose the best
refinement; and put the literals that were added to the original clause
to form this refinement in the node.
At this point it is clear that a lot of computational redundancy
exists if each refinement is evaluated separately. Indeed all
refinements contain exactly the same literals except those added
during this single refinement step. Organising all refinements into one
query pack, we obtain a query pack that essentially has only one
level (the root immediately branches into leaves).
When TILDE's lookahead facility is used [4], refinements
form a lattice and the query pack may contain multiple (though usually
few) levels.
Note that the root of these packs may consist of a conjunction of many
literals, giving the pack a broom-like form. The more literals in the
root of the pack, the greater the benefit of query pack execution is
expected to be.
Example 4
Assume the node currently being refined has the following query
associated with it:
?- circle(A,C),leftof(A,C,D),above(A,D,E),
i.e., the node covers all examples
where there is a circle to the
left of some other object which is itself above yet another object.
The query pack generated for this refinement could for instance be
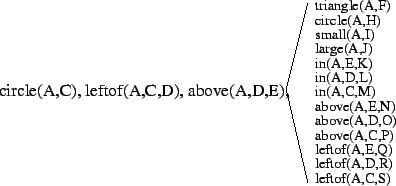
When evaluating this pack, all backtracking through the root of the
pack (the ``stick'' of the broom) will happen only once, instead of
once for each refinement. In other words: when evaluating queries one
by one, for each query the Prolog engine needs to search once again
for all objects 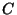 ,
,  and
and  fulfilling the constraint circle(A,C), leftof(A,C,D), above(A,D,E); when executing a pack
this search is done only once.
fulfilling the constraint circle(A,C), leftof(A,C,D), above(A,D,E); when executing a pack
this search is done only once.


Next: Other Algorithms Based on
Up: Refinement of a Single
Previous: Refinement of a Single
Hendrik Blockeel
2002-02-26
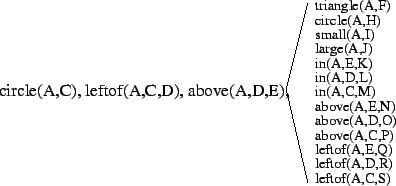
![]() ,
, ![]() and
and ![]() fulfilling the constraint circle(A,C), leftof(A,C,D), above(A,D,E); when executing a pack
this search is done only once.
fulfilling the constraint circle(A,C), leftof(A,C,D), above(A,D,E); when executing a pack
this search is done only once.