Allocation Strategy

As is evident from Section 3.1, ATTac-2000 relies heavily on computing the current most profitable allocation of goods to clients, G^*. Since G^* changes as prices change, ATTac-2000 needs to recompute it at every bidding opportunity. By using an integer linear programming approach, ATTac-2000 was able to compute optimal final allocations in every game instance during the tournament finals--one of only 2 entrants to do so.²

Most TAC participants used some form of greedy strategy for allocation [Greenwald StoneGreenwald Stone2001]. It is computationally feasible to quickly determine the maximum utility achievable by client 1 given a set of purchased goods, move on to client 2 with the remaining goods, etc. However, the greedy strategy can lead to suboptimal solutions. For example, consider 2 clients A and B with identical travel days IAD and IDD as well as identical entertainment values EV, but with A's $GHV = \$50$ and B's $GHV = \$150$. If the agent has exactly one of each type of hotel room for each day, the optimal assignment is clearly to assign the BGH to client B. However, if client A's utility is optimized first, it will be assigned the BGH, leaving B to stay in LFI. The agent's resulting score would be 100 less than it could have been.

As an improvement over the basic greedy strategy, we implemented a heuristic approach that implements the greedy strategy over 100 random client orderings and chooses the most profitable resulting allocation. Empirically, the resulting allocation is often optimal, and never far from optimal. In addition, it is always very quick to compute. In a set of seven games from just before the tournament, the greedy allocator was run approximately 600 times and produced allocations that averaged 99.5% of the optimal value.

As the competition drew near, however, it became clear that every point would count. We therefore implemented an allocation strategy that is guaranteed to find the optimal allocation of goods.³ The integer linear programming approach used by ATTac-2000 works by defining a set of variables, constraints on these variables, and an objective function. An assignment to the variables represents an allocation to the clients and the constraints ensure that the allocation is legal. The objective function encodes the fact that we seek the allocation with maximum value (utility minus cost).

The following notation is needed to describe the integer linear program. The formal notation is included for completeness; an equivalent English description follows each equation. The symbol cis a client (1 through 8). The symbol f is a feasible travel package, which consists of: the arrival day AD(f) (1 through 4); the departure day DD(f) (2 through 5), and the choice of hotel H(f)(BGH or LFI). There are 20 such travel packages. Symbol e is an entertainment ticket, which consists of: the day of the event D(e)(1 through 4), and the type of the event T(e) (baseball b, symphony s, or theater t). There are 12 different entertainment tickets. Symbol r is a resource (AD, DD, BGH, or LFI).

Using this notation, the 272 variables are: P(c,f), which indicates whether client c will be allocated feasible travel package f (160 variables); E(c,e), which indicates whether client c will be allocated entertainment ticket e (96 variables); and, B_r(d) is the number of copies of resource r we would like to buy for day d(16 variables).

There are also several constants that define the problem: o_r(d) is the number of tickets of resource r currently owned for day d, p_r(d) is the current price for resource r on day d, u_P(c,f)is utility to customer c for travel package f, and u_E(c,e) is the utility to customer c for entertainment ticket e.

Given this notation, the objective is to maximize utility minus cost

$$\sum_{c,f} u_P(c,f) P(c,f) + \sum_{c,e} u_E(c,e) E(c,e)$$

$$- \sum_{d\in\{2,3,4,5\}} p_{DD}(d) B_{DD}(d)$$

$$- \sum_{d\in\{1,2,3,4\},r\in\{{\rm BGH},{\rm LFI}, AD\}} p_r(d) B_r(d)$$

subject to the following 188 constraints:

• For all c, $\sum_{f} P(c,f) \le 1$: No client gets more than one travel package (8 constraints).
• For all $d \in \{1,2,3,4\}$,
  
  $$\sum_c \sum_{f\vert AD(f)=d} P(c,f) \le o_{AD}(d) + B_{AD}(d),$$
  
  
  For all $d \in \{1,2,3,4\}$ and $h\in\{{\rm BGH}, {\rm LFI}\}$,
  
  $$\sum_c \sum_{f\vert H(f)=h\ \& \ AD(f) \le d < DD(f)} P(c,f) \le o_h(d) + B_h(d),$$
  
  
  For all $d \in \{2,3,4,5\}$,
  
  $$\sum_c \sum_{f\vert DD(f)=d} P(c,f) \le o_{DD}(d) + B_{DD}(d):$$
  
  
  The demand for resources from the selected travel packages must not exceed the sum of the owned and bought resources (16 constraints).
• For all e, $\sum_{c} E(c,e) \le o_E(e)$: The total quantity of each entertainment ticket allocated does not exceed what is owned (12 constraints).
• For all c and e, $\sum_{f\vert AD(f) \le D(e) < DD(f)} P(c,f) \ge E(c,e)$: An entertainment ticket can only be used if its day is between the arrival and departure day of the selected travel package (96 constraints).
• For all c and $d \in \{1,2,3,4\}$, $\sum_{e\vert D(e)=d} E(c,e) \le 1$: Each client can only use one entertainment ticket per day (32 constraints).
• For all c and $y \in \{b,s,t\}$, $\sum_{e\vert T(e)=y} E(c,e) \le 1$: Each client can only use each type of entertainment ticket once (24 constraints).
• All variables are integers.

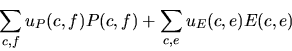
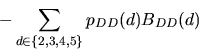
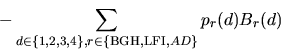
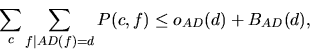
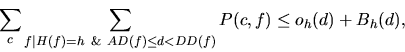
The solution to the resulting integer linear program is a value-maximizing allocation of owned resources to customers along with a list of resources that need to be purchased. Using the linear programming package ``LPsolve'', ATTac-2000 is usually able to find the globally optimal solution in under one second on a 650 MHz Pentium II.

Note that this is not by any means the only possible formulation of the allocation. boyan01 boyan01 studied a variant and found that it performed extremely well on a collection of large, random allocation problems.

The above approach is guaranteed to find the optimal allocation, and usually does so quickly. However, since integer linear programming is an NP-complete problem, some inputs can lead to significantly longer solution times. In a sample of 32 games taken shortly before the finals, the allocator was called 1866 times. In 93% of the cases, the optimization took a second or less. Less than 1% took 6 or more seconds. However, the 3 longest running times were all over a minute and all came from the same game. ATTac-2000 used the strategy that if an integer linear program takes 6 or more seconds to solve, the above-mentioned greedy strategy over random client orderings is used as a fall-back strategy for the rest of the game. This fall-back strategy was not needed during the tournament finals.