

Next: ATTac-2000
Up: ATTac-2000: An Adaptive Autonomous
Previous: Introduction
TAC
A TAC game instance pits 8 autonomous bidding agents against one
another. Each TAC agent is a simulated travel agent with 8 clients,
each of whom would like to travel from TACtown to Boston and back
again during a common 5-day period. Each client is characterized by a
random set of preferences for the possible arrival and departure
dates; hotel rooms (The Grand Hotel and Le Fleabag Inn); and
entertainment tickets (symphony, theater, and baseball). To obtain
utility for a client, an agent must construct a travel package for
that client by purchasing airline tickets to and from TACtown and
securing hotel reservations; it is possible to obtain additional
utility by providing entertainment tickets as well. A TAC agent's
score in a game instance is the difference between the sum of its
clients' utilities for the packages they receive and the agent's total
expenditure.
TAC agents buy flights, hotel rooms and entertainment tickets in
different types of auctions. The TAC server, running at the
University of Michigan, maintains the markets and sends price quotes to the agents. The agents connect over the Internet and send
bids to the server that update the markets accordingly and execute
transactions.
Each game instance lasts 15 minutes and includes a total of 28
auctions of 3 different types.
- Flights (8 auctions):
- There is a separate auction for each type
of airline ticket: flights to Boston (inflights) on days 1-4
and flights from Boston (outflights) on days 2-5. There is
an unlimited supply of airline tickets, and their ask price
periodically increases or decreases randomly by from
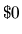 to
to  .
In all
cases, tickets are priced between
.
In all
cases, tickets are priced between 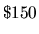 and
and  .
When the
server receives a bid at or above the ask price, the transaction is
cleared immediately at the ask price. No resale of
airline tickets is allowed.
.
When the
server receives a bid at or above the ask price, the transaction is
cleared immediately at the ask price. No resale of
airline tickets is allowed.
- Hotel Rooms (8):
- There are two different types of hotel
rooms--the Boston Grand Hotel (BGH) and Le Fleabag Inn (LFI)--each
of which has 16 rooms available on days 1-4. The rooms are sold
in a 16th-price ascending (English) auction, meaning that for
each of the 8 types of hotel rooms, the 16 highest bidders get the
rooms at the 16th highest price. For example, if there are 15 bids
for BGH on day 2 at
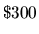 ,
2 bids at
,
2 bids at 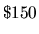 ,
and any number of
lower bids, the rooms are sold for
,
and any number of
lower bids, the rooms are sold for 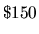 to the 15 high bidders plus
one of the
to the 15 high bidders plus
one of the 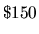 bidders (earliest received bid). The ask price is
the current 16th-highest bid. Thus, agents have no knowledge of, for
example, the current highest bid. New bids must be higher than the
current ask price. No bid withdrawal and no resale is
allowed. Transactions only clear when the auction closes. To
prevent agents from all waiting until the end of the game to bid on
hotel rooms, hotel auctions can close after an unspecified period
(roughly one minute) of inactivity (no new bids received).
bidders (earliest received bid). The ask price is
the current 16th-highest bid. Thus, agents have no knowledge of, for
example, the current highest bid. New bids must be higher than the
current ask price. No bid withdrawal and no resale is
allowed. Transactions only clear when the auction closes. To
prevent agents from all waiting until the end of the game to bid on
hotel rooms, hotel auctions can close after an unspecified period
(roughly one minute) of inactivity (no new bids received).
- Entertainment Tickets (12):
- Baseball, symphony, and theater
tickets are each sold for days 1-4 in continuous double
auctions. Here, agents can buy and sell tickets, with
transactions clearing immediately when one agent places a buy
bid at a price at least as high as another agent's sell price. Unlike
the other auction types in which the goods are sold from a centralized
stock, each agent starts with a random endowment of entertainment
tickets. The prices sent to agents are the bid-ask spreads,
i.e., the highest current bid price and the lowest current ask price
(due to immediate clears, ask price is always greater than bid price).
When a bid that beats the current bid (ask) price arrives, the sale
price is the standing bid (ask) price, as opposed to the arriving ask
(bid) price. In this case, bid withdrawal and ticket
resale are both permitted.
In addition to unpredictable market prices, other sources of
variability from game instance to game instance are the client
profiles assigned to the agents and the random initial allotment of
entertainment tickets. Each TAC agent has 8 clients with randomly
assigned travel preferences. Clients have parameters for ideal
arrival day, IAD (1-4); ideal departure day, IDD (2-5); grand hotel value, GHV (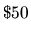 -
-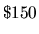 ); and
entertainment values, EV (
); and
entertainment values, EV (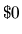 -
- )
for each type of
entertainment ticket.
)
for each type of
entertainment ticket.
The utility obtained by a client is determined by the travel package
that it is given in combination with its preferences. To obtain a
non-zero utility, the client must be assigned a feasible travel
package consisting of an arrival day AD with the corresponding
inflight, departure day DD with the corresponding outflight, and
hotel rooms of the same type (BGH or LFI) for each day d such
that
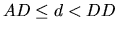 .
At most one entertainment ticket can be
assigned for each day
.
At most one entertainment ticket can be
assigned for each day
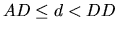 ,
and no client can be given
more than one of the same entertainment ticket type. Given a feasible
package, the client's utility is defined as
,
and no client can be given
more than one of the same entertainment ticket type. Given a feasible
package, the client's utility is defined as
where
- travelPenalty =

- hotelBonus = GHV if the client is in the GBH,
0 otherwise.
- funBonus = sum of relevant EV's for each
entertainment ticket type assigned to the client.
A TAC agent's final score is simply the sum of its clients' utilities
minus the agent's expenditures. Throughout the game instance, it must
decide what bids to place in each of the 28 auctions. At the end of
the game, it must submit a final allocation of purchased goods to its
clients.
The client preferences, allocations, and resulting utilities from one
particular game from the TAC finals (Game 3070 on the TAC server) are
shown in Tables 1 and 2.
Table 1:
ATTac-2000's client preferences from game 3070. BEV,
SEV, and TEV are EVs for baseball, symphony, and
theater respectively.
| Client |
IAD |
IDD |
GHV |
BEV |
SEV |
TEV |
| 1 |
Day 2 |
Day 5 |
73 |
175 |
34 |
24 |
| 2 |
Day 1 |
Day 3 |
125 |
113 |
124 |
57 |
| 3 |
Day 4 |
Day 5 |
73 |
157 |
12 |
177 |
| 4 |
Day 1 |
Day 2 |
102 |
50 |
67 |
49 |
| 5 |
Day 1 |
Day 3 |
75 |
12 |
135 |
110 |
| 6 |
Day 2 |
Day 4 |
86 |
197 |
8 |
59 |
| 7 |
Day 1 |
Day 5 |
90 |
56 |
197 |
162 |
| 8 |
Day 1 |
Day 3 |
50 |
79 |
92 |
136 |
|
Table 2:
ATTac-2000's client allocations and utilities from game 3070.
Client 1's ``B4'' under ``Ent'ment'' indicates baseball on day 4.
| Client |
AD |
DD |
Hotel |
Ent'ment |
Utility |
| 1 |
Day 2 |
Day 5 |
LFI |
B4 |
1175 |
| 2 |
Day 1 |
Day 2 |
BGH |
B1 |
1138 |
| 3 |
Day 3 |
Day 5 |
LFI |
T3, B4 |
1234 |
| 4 |
Day 1 |
Day 2 |
BGH |
None |
1102 |
| 5 |
Day 1 |
Day 2 |
BGH |
S1 |
1110 |
| 6 |
Day 2 |
Day 3 |
BGH |
B2 |
1183 |
| 7 |
Day 1 |
Day 5 |
LFI |
S2, B3, T4 |
1415 |
| 8 |
Day 1 |
Day 2 |
BGH |
T1 |
1086 |
|
For full details on the design and mechanisms of the TAC server,
see WellmanTAC00 WellmanTAC00.


Next: ATTac-2000
Up: ATTac-2000: An Adaptive Autonomous
Previous: Introduction
Peter Stone
2001-09-13
![]() -
-![]() ); and
entertainment values, EV (
); and
entertainment values, EV (![]() -
-![]() )
for each type of
entertainment ticket.
)
for each type of
entertainment ticket.
![]() .
At most one entertainment ticket can be
assigned for each day
.
At most one entertainment ticket can be
assigned for each day
![]() ,
and no client can be given
more than one of the same entertainment ticket type. Given a feasible
package, the client's utility is defined as
,
and no client can be given
more than one of the same entertainment ticket type. Given a feasible
package, the client's utility is defined as