

Next: Computing the of two
Up: An Efficient Representation and
Previous: Computing the Span of
Given an Allen relation r and a set I of intervals, let  denote
the set J of all intervals
denote
the set J of all intervals 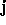 such that
such that  for some
for some 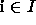 .
Given an Allen relation r and a normalized spanning interval
.
Given an Allen relation r and a normalized spanning interval  , let
, let
 denote a set of normalized spanning intervals whose extension is
denote a set of normalized spanning intervals whose extension is
 , where I is the extension of
, where I is the extension of  .
One can compute
.
One can compute  as follows:
as follows:

An important property of normalized spanning intervals is that for any
normalized spanning interval  ,
,  contains at most 1, 4, 4,
2, 2, 4, 4, 2, 2, 2, 2, 4, or 4 normalized spanning
intervals when r is =, <, >,
contains at most 1, 4, 4,
2, 2, 4, 4, 2, 2, 2, 2, 4, or 4 normalized spanning
intervals when r is =, <, >,  ,
,  ,
, 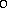 ,
,
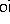 ,
, 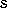 ,
, 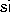 ,
, 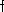 ,
,  ,
, 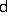 ,
or
,
or  respectively.
In practice, however, fewer normalized spanning intervals are needed, often
only one.
respectively.
In practice, however, fewer normalized spanning intervals are needed, often
only one.
The intuition behind the above definition is as follows.
Let us handle each of the cases separately.
- r=<
- For any intervals
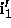 and
and  in the extensions of
in the extensions of 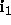 and
and  respectively we want
respectively we want  .
From (2) we get
.
From (2) we get  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  .
Combining these we get
.
Combining these we get
 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.
- r=>
- For any intervals
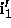 and
and  in the extensions of
in the extensions of 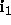 and
and  respectively we want
respectively we want  .
From (3) we get
.
From (3) we get  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  .
Combining these we get
.
Combining these we get
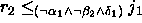 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.
-

- For any intervals
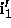 and
and  in the
extensions of
in the
extensions of 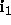 and
and  respectively we want
respectively we want
 .
From (4) we get
.
From (4) we get 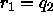 and
and  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 .
Combining these we get
.
Combining these we get
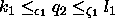 and
and  .
In this case, only
.
In this case, only  is free indicating that the upper endpoint
of
is free indicating that the upper endpoint
of  can be open or closed.
can be open or closed.
-

- For any intervals
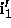 and
and  in the
extensions of
in the
extensions of 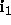 and
and  respectively we want
respectively we want
 .
From (5) we get
.
From (5) we get  and
and  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 .
Combining these we get
.
Combining these we get
 and
and  .
In this case, only
.
In this case, only  is free indicating that the lower endpoint
of
is free indicating that the lower endpoint
of  can be open or closed.
can be open or closed.
-

- For any intervals
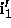 and
and  in the
extensions of
in the
extensions of 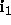 and
and  respectively we want
respectively we want
 .
From (6) we get
.
From (6) we get
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  and
and
 .
Combining these we get
.
Combining these we get
 and
and
 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.
-
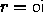
- For any intervals
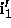 and
and  in the
extensions of
in the
extensions of 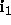 and
and  respectively we want
respectively we want
 .
From (7) we get
.
From (7) we get
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  and
and
 .
Combining these we get
.
Combining these we get
 and
and
 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.
-

- For any intervals
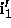 and
and  in the
extensions of
in the
extensions of 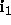 and
and  respectively we want
respectively we want
 .
From (8) we get
.
From (8) we get 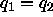 ,
,  , and
, and
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 and
and  .
Combining these we get
.
Combining these we get  ,
,
 , and
, and
 .
In this case, only
.
In this case, only  is free indicating that the upper endpoint
of
is free indicating that the upper endpoint
of  can be open or closed.
can be open or closed.
-

- For any intervals
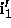 and
and  in the
extensions of
in the
extensions of 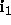 and
and  respectively we want
respectively we want
 .
From (9) we get
.
From (9) we get 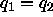 ,
,  , and
, and
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 and
and  .
Combining these we get
.
Combining these we get  ,
,
 , and
, and
 .
In this case, only
.
In this case, only  is free indicating that the upper endpoint
of
is free indicating that the upper endpoint
of  can be open or closed.
can be open or closed.
-

- For any intervals
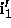 and
and  in the
extensions of
in the
extensions of 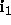 and
and  respectively we want
respectively we want
 .
From (10) we get
.
From (10) we get 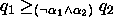 ,
,
 , and
, and  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 and
and  .
Combining these we get
.
Combining these we get  ,
,
 , and
, and
 .
In this case, only
.
In this case, only  is free indicating that the lower endpoint
of
is free indicating that the lower endpoint
of  can be open or closed.
can be open or closed.
-
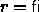
- For any intervals
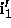 and
and  in the
extensions of
in the
extensions of 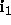 and
and  respectively we want
respectively we want
 .
From (11) we get
.
From (11) we get 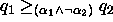 ,
,
 , and
, and  .
Furthermore, from (14) we get
.
Furthermore, from (14) we get
 and
and  .
Combining these we get
.
Combining these we get  ,
,
 , and
, and
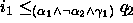 .
In this case, only
.
In this case, only  is free indicating that the lower endpoint
of
is free indicating that the lower endpoint
of  can be open or closed.
can be open or closed.
-

- For any intervals
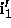 and
and  in the
extensions of
in the
extensions of 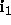 and
and  respectively we want
respectively we want
 .
From (12) we get
.
From (12) we get 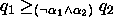 and
and
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  and
and
 .
Combining these we get
.
Combining these we get
 and
and
 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.
-

- For any intervals
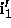 and
and  in the
extensions of
in the
extensions of 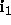 and
and  respectively we want
respectively we want
 .
From (13) we get
.
From (13) we get  and
and
 .
Furthermore, from (14) we get
.
Furthermore, from (14) we get  and
and
 .
Combining these we get
.
Combining these we get
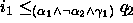 and
and
 .
In this case, both
.
In this case, both  and
and  are free indicating that either
endpoint of
are free indicating that either
endpoint of  can be open or closed.
can be open or closed.


Next: Computing the of two
Up: An Efficient Representation and
Previous: Computing the Span of
Jeffrey Mark Siskind
Wed Aug 1 19:08:09 EDT 2001
![]() denote
the set J of all intervals
denote
the set J of all intervals ![]() such that
such that ![]() for some
for some ![]() .
Given an Allen relation r and a normalized spanning interval
.
Given an Allen relation r and a normalized spanning interval ![]() , let
, let
![]() denote a set of normalized spanning intervals whose extension is
denote a set of normalized spanning intervals whose extension is
![]() , where I is the extension of
, where I is the extension of ![]() .
One can compute
.
One can compute ![]() as follows:
as follows:

![]() ,
, ![]() contains at most 1, 4, 4,
2, 2, 4, 4, 2, 2, 2, 2, 4, or 4 normalized spanning
intervals when r is =, <, >,
contains at most 1, 4, 4,
2, 2, 4, 4, 2, 2, 2, 2, 4, or 4 normalized spanning
intervals when r is =, <, >, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
or
,
or ![]() respectively.
In practice, however, fewer normalized spanning intervals are needed, often
only one.
respectively.
In practice, however, fewer normalized spanning intervals are needed, often
only one.