Retaining Uniform Improvability

To address convergence issues, we assume that the input to point-based DP update is uniformly improvable and require its output to be also uniformly improvable. We will explain later how the assumption can be facilitated and how the requirement guarantees convergence of the modified value iteration algorithm. In this subsection, we discuss how the requirement can be fulfilled.

Point-based DP update constructs new vectors by backing up on belief points and the new vectors are all members of . Hence the output of point-based DP update is trivially dominated by . If the output also dominates , then it must be uniformly improvable by Lemma 2. The question is how to guarantee that the output dominates .

Consider the set resulted from backUpWitnessPoints. If it does not dominate , then there must exist a belief state b such . Consequently, there must exist a vector in such that . This gives us the following subroutine for testing whether dominates and for, when this is not the case, adding vectors to so that it does. The subroutine is called backUpLPPoints because belief points are found by solving linear programs.

 
 		    :

		1.  		 for each   

		2.  		  		  do {

		3.  		  		  		     .

		4.  		  		  		   if   ,

		5.  		    		   		  		  	   .

		6.  		    		   		  		  	   .

		7.   		   		  		   		   .

		8.  		  		  } while (  ).

The subroutine examines vectors in one by one. For each in , it calls another subroutine dominanceCheck to try to find a belief point b such that . If such a point is found, it backs up on it, resulting in a new vector (line 5). By the property of the backup operator, b is a witness point of w.r.t (line 6). There cannot be any vector in that equals . Consequently, the vector is simply added to without checking for duplicates (line 7). The process repeats for until dominanceCheck returns NULL, that is when there are no belief points b such that . When backUpLPPoints terminates, we have for any vector in and any belief point b. Hence dominates .

The subroutine first checks whether there exists a vector in that pointwise dominates , that is for all states s. If such an exists, it returns NULL right away. Otherwise, it solves the following linear program . It returns the solution point b when the optimal value of the objective function is positive and returns NULL otherwise:

 
			LP  :

			1.		  Variables: x, b(s) for each state s

                 2.		       Maximize: x.

                 3. 		      Constraints:

                 4.		 		          
                                for all    

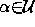
                  5. 				       ,     for all
                                states s.