Introduction

During the last years a large number of formalisms for knowledge representation (KR) have been proposed in the literature. Such formalisms have been studied from several perspectives, including semantical properties, and computational complexity. Here we investigate space efficiency, a property that has to do with the minimal size needed to represent a certain piece of knowledge in a given formalism. This study is motivated by the fact that the same piece of knowledge can be represented by two formalisms using a different amount of space. Therefore, all else remaining the same, a formalism could be preferred over another one because it needs less space to store information.

The definition of space efficiency, however, is not simple. Indeed, a formalism may allow several different ways to represent the same piece of knowledge. For example, let us assume that we want to represent the piece of knowledge ``today is Monday''. In Propositional Logic we may decide to use a single propositional variable $monday$. The fact that today is Monday can be represented by the formula $monday$, but also by the formula $\neg \neg monday$, as well as $monday \wedge (rain \vee \neg rain)$, because all formulae of the Propositional Logic that are logically equivalent to $monday$ represent exactly the same information.

In Propositional Logic, we should consider the shortest of the equivalent formulae used to represent the information we have. The same principle can be applied to a generic formalism: if it allows several formulae to represent the same information, then we only take into account the shortest one. Therefore, we say that the space efficiency of a formalism $F$ in representing a certain piece of knowledge $\alpha$ is the size of the shortest formula of $F$ that represents $\alpha$. Space efficiency --also called succinctness or compactness-- of a formalism is a measure of its ability in representing knowledge in a small amount of space.

In this paper we focus on propositional KR (PKR) formalisms. We do not give a formal definition of which formalisms are propositional and which one are not: intuitively, in a propositional formalism, quantifications are not allowed, and thus the formulae are syntactically bounded to be formed only using propositional connectives, plus some other kind of nonclassical connectives (for instance, negation in logic programs, etc.).

So far, we have not discussed what knowledge represents. A possible way to think of a piece of knowledge is that it represents all facts that can be inferred from it. In other words, knowing something is the same as knowing everything that can be logically implied. The second way -- which is in some cases more natural -- is to think of a piece of knowledge as the set of states of the world that we consider possible.

In a more formal way, we say that knowledge is represented either by a set of propositional interpretations (those describing states of the world we consider plausible) or a set of formulae (those implied from what we know). Consequently, we focus on both reasoning problems of model checking and theorem proving. The following example shows that we can really think of knowledge in both ways.

Example 1   We want to eat in a fast food, and want to have either a sandwich or a salad (but not both), and either water or coke (but not both).

In Propositional Logic, each choice can be represented as a model, and the following models represent all possible choices (models are represented by writing down only the letters mapped to true).

$$A = \{ \{\mbox{sandwich},\mbox{water}\}, \{\mbox{sandwich},... ...{\mbox{salad},\mbox{water}\}, \{\mbox{salad},\mbox{coke}\} \}$$

For representing the set of choices we can use formulae instead of models. In this case, we write down a set of formulae whose models represent exactly the allowed choices, as follows.

$$\begin{eqnarray*} C &=& (\mbox{sandwich}\vee \mbox{salad}) \wedge (\neg \mbox{s... ...vee \neg \mbox{coke}) \wedge (\neg \mbox{coke}\rightarrow water) \end{eqnarray*}$$

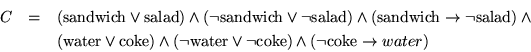
Actually, we can get rid of redundancies, and end up with the following formula.

$$F = (\mbox{sandwich}\vee \mbox{salad}) \wedge (\neg \mbox{s... ...e \mbox{coke}) \wedge (\neg \mbox{water}\vee \neg \mbox{coke})$$

More formally, $F$ represents the set of models $A$, because for each interpretation $I$, $I \in A$ holds if and only if $I \models F$. The formula $F$ also represents the set of formulae $C$, because $Cn(F) = Cn(C)$, where $Cn(.)$ is the function that gives the set of all conclusions that can be drawn from a propositional formula.