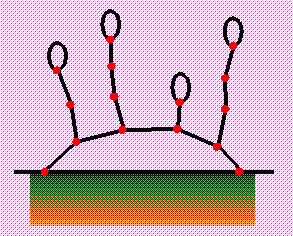
 has two components], but nor can they be connected, else we
fall foul of the `three route' rule because they are also
connected at the ground, by the previous result.
has two components], but nor can they be connected, else we
fall foul of the `three route' rule because they are also
connected at the ground, by the previous result.
Impartial Hackenbush can be completely solved by the three results:
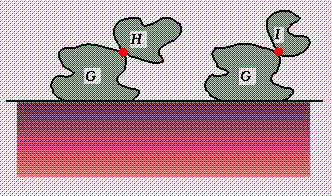
Proof: Play the difference game, G:H-G:I. [For impartial games, equal to their own negatives, the difference game is the same as the disjunctive sum of the games.] Since H-I = 0, to every move in either H or -I there is a winning reply in H-I; this same winning reply can be played in response to a move in the colon'ed version, and then we can appeal to induction, as the resulting picture is a simpler one to which the colon principle still applies. Equally a move in G has a symmetric counter in -G and vice versa; this move and counter either delete the articulation points and all that sail on them in both components [giving a zero game] or in neither, in which case we can again appeal to induction and the colon principle.Note that this works perfectly well even in general Hackenbush, but we need it here only in the impartial version. In the impartial version, the value of H will perforce be a nimber, so the component I might just as well be a `snake', a simple chain of n edges, n>=0, value *n, of the appropriate length. In the particular case where G is just a single edge, this shows that G:H is equivalent to a snake of length n+1, which is the tree principle.
 has two components], but nor can they be connected, else we
fall foul of the `three route' rule because they are also
connected at the ground, by the previous result.
has two components], but nor can they be connected, else we
fall foul of the `three route' rule because they are also
connected at the ground, by the previous result.
 So we need to show that a picture typified by this one has value zero,
i.e. is a first-player loss.
Clearly any move in any snake loses;
the other player can make the same move in the corresponding snake,
to give a simpler bridge, which must be good [or we can use induction].
So we need to show that a picture typified by this one has value zero,
i.e. is a first-player loss.
Clearly any move in any snake loses;
the other player can make the same move in the corresponding snake,
to give a simpler bridge, which must be good [or we can use induction].
What about moves in the bridge, typified by the greyed-out edge? These too lose. Such a move creates two trees. Recall that to evaluate a tree, we have to Nim-add branches, add one to go down, Nim-add, add one, etc. As Nim addition is adding without carry, the least-significant [binary] digit works out the same whether we Nim-add or ordinary-add; in other words, if we replace all the Nim-adds by ordinary-adds, the parity of the answer will be the same. From this, it is easily seen that the parity of the value of the tree is the same as the parity of its number of edges. Now, whether we started out with an odd or an even bridge, that bridge plus its fused version has an even number of edges [each snake occurs twice, and there is a blade of grass only if the number of spans is odd]. So when we chop a span, we have an odd number of edges; we have just demolished the last loop, so the whole picture is the Nim-sum of a collection of trees, and so is an odd nimber, so cannot be zero. In other words, any move in the bridge creates a picture which is a win for the other player.
That completes the result in the case where the bridge is even. When the bridge is odd, as in the picture shown, there is one final move, to mow the grass. The resulting picture has an odd number of edges, but it isn't a tree. Any chop of a bridge span will create trees with, in total, an even number of edges, but they could possibly all be *2 or *4 or whatever. Can we move in a snake? Well, if any snake on the bridge is odd, then chop off its head. The resulting picture is good [as it is simpler than the one we started with], so its value is lots of snakes that cancel out in pairs, an odd bridge that fuses to *1, the original odd snake from the ground worth *(2n+1) and the chopped snake from the bridge worth *(2n), total zero, so the chop was a good reply. So, we are left with the case where they are all even.
We finally have to show that in a bridge with an odd number of spans and a collection of even snakes, plus copies of all the snakes, there is a move to zero. Call the centre span `white', and then label spans alternately black and white out towards the ends of the bridge. It suffices to show that we can win by chopping some white span. Suppose we chop such a span. What is the resulting value of the two trees? Well, each has Nim-value
2a + 1 @ 2b + 1 @ 2c + 1 @ 2d + 1 @ ...[where `@' means Nim addition and lots of parentheses have been omitted, but the expression should be worked out strictly from left to right], where 2a, 2b, ... are the snake heights working out from the chopped edge. But now if you look at the way the odds and evens go, the first, third, fifth, ... `+ 1' have the same effect as `@ 1', which means that they commute with the next `@ 2b', and the sum is the same as the nimber
2a @ 2b + 2 @ 2c @ 2d + 2 @ ...Now, everything in this is even, so the result is twice the result of
a @ b + 1 @ c @ d + 1 @ ...But this is what you get if you halve each snake, then close up each black span to a point, Nim-adding the snakes at each end. [Each of the trees has a black span at its end, as we chopped a white span.] The resulting picture is good, and clearly has Nim-value 1, [or game value *1 = *]. [It has lots of snakes that can be paired off, and an odd-span bridge, as there are an odd number of white spans.] So, some move in the reduced bridge wins, i.e. chops it to zero, and therefore the corresponding move in the original bridge also chops to [twice] zero. That concludes the proof.
The very astute will have noted a flaw: The win in the reduced bridge might not be by chopping a bridge span, but by chopping a snake. The fusion principle, as applied to the simpler picture, shows that you can in fact chop a bridge span instead, but finding which one is decidedly non-trivial. The way to proceed is a generalisation of the above `black-white' idea; for `how to do it', see Winning Ways, p189.None of the above is examinable!
 E-mail me.
E-mail me.
 My home page.
My home page.
 The University of Nottingham.
The University of Nottingham.