Scribe Notes -- January 26, 1998

Slide 1 Slide 1: FPGA Arithmetic II
Arithmetic is important in realms where DSPs are traditionally applied.
Slide 2 Slide 2: The Wallace Tree
Once the partial products are computed, adding them takes time.  A tree of partial products is built to add them together.  Full adders in this tree take 3 bits from each column and generate a sum and carry bit.  The carry bit goes into the more significant position in the result, and the sum goes into the less significant bit.
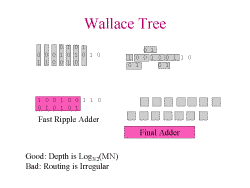Slide 3 Slide 3: Wallace Tree
This reduction of bits is repeated until the multiplication is complete. If there are 2 bits in a column, a half adder is used instead of a full adder.  The advantage of a Wallace tree over other adders is that the critical path is no longer linear with the number of bits, it is log3/2 instead: this is because each stage reduces 3 bits to 2 bits. The critical path is down the diagonal and accross the bottom adder. This circuit can not use the fast carry logic effectively because many blocks have 2 carry ins. The routing of this is irregular, making it difficult to fit in an FPGA nicely. Multiply and add can be implemented with little incremental cost over just a multiply, because the add can be integrated into the Wallace tree.
Slide 4 Slide 4: Partial Product Generation
Using AND gates for partial product generation wastes LUT resources. The AND gate may not be subsumed into the LUT. Use small multipliers.
Slide 5 Slide 5: CSD Vectors
Binary encoding has each bit represent a number of the form {0,1}2n.  CSD encoding uses {-1,0,1}2n.  To encode this: C = (B + (B<<1)).  -2C is C shifted 1 to the right and multiplied by 2.  So the final result, D, contains -1's, 0's and 1's. For an n bit number, there can only be n/2 non-zero digits in a CSD expression.
Slide 6 Slide 6: Booth Encoding
The digits of the encoded number,  E,  are one of {1,0,-1,-2}.  Each bit position in E corresponds to (..., 26, 24, 22, 20), unlike binary where they are (..., 28, 24, 22, 20).  Each digit in E is computed by selecting a group of 3 digits in the original number, adding the two least significant bits, and then subtracting 2 times the most significant bit.  In this example, E = 26-22+20.
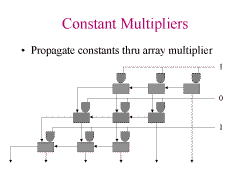Slide 7 Slide 7: Constant Multipliers
Can eliminate adders with 0's on the inputs. This can drastically reduce the number of adders. In addition, the and gates can be eliminated.
Slide 8 Slide 8: Constant Multipliers
CSD reduces the complexity of a multiplier by encoding a multiply as an add followed by a subtract. i.e. 101111 = 110000 - 000001.  Common sub-expressions reduce the amount of circuitry required at the expense of having more wires.
Slide 9 Slide 9: LUT-Based Constant Multipliers
A 4 bit constant with a 4 bit operand produces an 8 bit product. An array of LUTs can be used to implement a 4->8 multiplier.
Slide 10 Slide 10: LUT-Based Constant Multipliers
This diagram shows the layout of a circuit that does the computation shown on the previous slide.  8 bits come in top of this diagram into 12 different 4-LUTs.  Each set of 4-LUTs produces 3 four bit vectors -- the three vectors on the left are added to the top two vectors on the right, and concatenated with the lower vector on the right.  This can be arranged in a tree structure for larger multipliers. An interesting point is that the constants can be changed in the LUT SRAM without changing the wiring to produce new constant multipliers.  This allows a single  constant multiplier to be dynamically loaded with new constants.
Slide 11 Slide 11: Distributed Arithmetic
Can be extended by taking more bits from the input at once, but this begins to look like a LUT based multiplier.
Slide 12 Slide 12: Distributed Arithmetic
This combination allows a convolution to be computed at the same time as performing the multiplication.
Slide 13 Slide 13: Why Floating Point?
Another reason is that FP may improve resiliance to quantization error.
Slide 14 Slide 14: Shirazi Paper
There are multiple errors in the paper, including: The algorithms presented do not account for the values 0, plus or minus infinity, or NaN.

Barrel Shift VHDL:

The barrel shifter should not have to be expanded into a unrolled loop. The initial implementation uses a linear chain of MUXs to perform the shifting, while the unrolled version uses a logarithmic number of layers. The log version should be expressible as a loop as well.
 

What is "Method 3 & 4?":

Using off chip RAM for looking up reciprocals is only practical in SPLASH. Not a general purpose solution.
 

Why not pipeline the addition?

This makes convolution harder, since multiple sums would be in the pipeline at once, and these sums would then have to be added themselves to complete the convolution.
Slide 15 Slide 15: Floating Point Multiplication
The size of the integer multiplier dominates the circuit, especially as n increases. The adder is the same size as the multiplier.
Slide 16 Slide 16: Floating Point Addition
Slide 17 Slide 17: Floating Point on FPGAs
What features would improve FP performance if they were on an FPGA? How expandable are these algorithms?
How about 32 bit FP?
Distribute accross FPGAs? Does this work?
How many bits are required to solve the problem at hand? Can a 12 bit FP FPGA beat a 64 bit Alpha?
Numbers such as NaN and infinity were ignored by this paper. How important are they? How much logic would be needed to handle them?
Crazy idea: Dynamic reconfiguration can be used instead of floating point. If an adder determines that the next stage of a calculation will overflow or underflow, have it reconfigure the next stage to use a different number of bits for computation, or for it to move its fixed decimal point left or right. Alternatively, if a calculation is using fixed coefficients, the compiler could figure out what precision to use at each stage of a calculation. The FIR filter was made using general purpose multipliers.
Why not use specialized multipliers at each stage?
Scribed by Chris Colohan