In this section, we present a randomized algorithm for routing any
permutation of N packets on an N-node shuffle-exchange graph in
steps using constant-size queues. The previous 
-time algorithms [2] required queues of size
.
Figure 4 shows an 8-node shuffle-exchange graph. Each
node is labeled with a unique 
-bit binary string.
A node labeled 
is linked to a node labeled 
by a shuffle
edge if rotating a one position to the left or right yields b,
i.e., if either 
or 
. Two nodes labeled a
and b are linked by an exchange edge if a and b differ
in only the least significant (rightmost) bit, i.e., 
. In the figure, the shuffle edges are solid,
and the exchange edges are dashed.
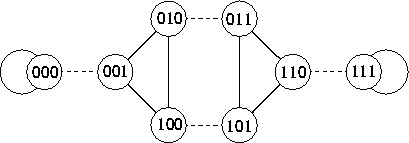
Figure 4: An 8-node shuffle-exchange
graph. Shuffle edges are solid, exchange edges dashed.
The removal of the exchange edges partitions the graph into a set of connected components called necklaces. Each necklace is a ring of nodes connected by shuffle edges. If two nodes lie on the same necklace, then their labels are rotations of each other. Due to cyclic symmetry, the number of nodes in the necklaces differ. For example, in a 64-node shuffle-exchange graph, the nodes 010101 and 101010 form a 2-node necklace, while 011011, 110110, and 101101 form a 3-node necklace. For each necklace, the node with the lexicographically minimum label is chosen to be the necklace's representative.