It is easier to establish edge-disjoint paths in R than node-disjoint paths. In particular, it is not necessary to apply the technique of [17] for tolerating faults in multibutterflies to the second and third parts of the network as we did in order to establish the node-disjoint paths. The main thing that must be done is to modify the algorithm from Section 4 for locking down node-disjoint paths in a multibutterfly so that it allows a constant number of edge-disjoint paths to pass through each node. Let r be the maximum number of paths that may pass through a node. In order to replace the unshared neighbors protocol with one that allows r paths to pass through a node, we define the following r-neighbors property for splitters. Similar definitions hold for mergers, or for pairs of consecutive levels like those in the first and fourth parts of R.
The following lemma shows that a splitter with a sufficient expansion property also has an r-neighbors property.
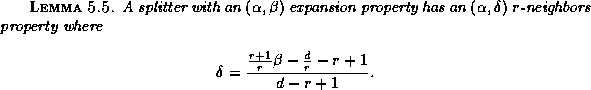
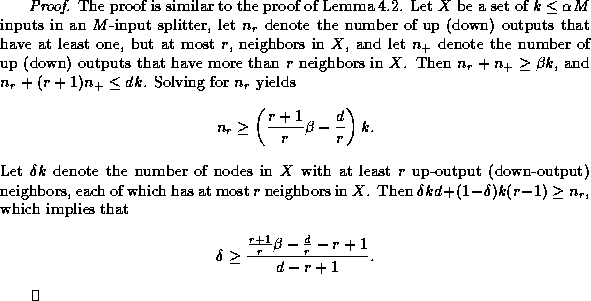
The algorithm for routing edge-disjoint paths in a multibutterfly is
nearly identical to the algorithm described in
Section 4 for routing node-disjoint paths. First,
each node that has at least one path to extend in either the up (or
down) direction sends a proposal to each of his output neighbors
in the up (down) direction. Then, every output node that receives at
most r proposals sends back acceptances to all of those proposals.
(Notice that this step limits the number of paths passing through a
node to at most r.) Finally, each node that receives enough
acceptances to extend all of its paths does so. In a network
with an 
r-neighbors property, a constant fraction
of the paths on each level are extended at each step. Thus, the time
to extend a set of N paths from one level to the next is 
, and the total time to route a set of N paths from the inputs to
the outputs is 
. As in Section 4, this
time can be improved to 
using place-holders and
cancellation signals.
Note that for 
, only 
expansion is required in order to have an 
r-unshared neighbors property, where 
and 
.
Since an algorithm for finding edge-disjoint paths can be converted to
an algorithm for finding node-disjoint paths by replacing each
degree-2d node with a 
complete bipartite graph, the
algorithm of this section reduces the expansion required for finding
either edge- or node-disjoint paths from 
to 
. The difference is important because explicit
constructions of expander graphs are known for 
[13], but not for 
. The algorithms for
tolerating faults in [17] and the algorithms for routing
paths in a nonblocking fashion in this paper still seem to require
. Recently, however, Pippenger has shown how to perform
all of these tasks using only expansion 
[31].
In order to use this routing algorithm in network R, we must make
one modification. The paths from the sources do not necessarily start
on level 
of the first part. In fact as many as four paths
may start at any node in the first part. (Recall that sources in the
second, third, and fourth parts start their paths in the first part.)
Thus, the routing algorithm must be modified so that a node in the
first part sends acceptances to the nodes at the previous level only
if it receives at most r-4 proposals. The impact on the performance
of the algorithm will be negligible if r is large relative to 4.