Bayesian Networks

Bayesian networks -- also known as "belief networks" or "causal networks" -- are graphical models for representing multivariate probability distributions. Each variable is represented as a vertex in an directed acyclic graph ("dag"); the probability distribution is represented in factorized form as follows:

where is the set of vertices that are 's parents in the graph. A Bayesian network is fully specified by the combination of:

• The graph structure, i.e., what directed arcs exist in the graph.
• The probability table for each variable .

A small example Bayesian network structure for a (somewhat facetious/futuristic) medical diagnostic domain is shown below. This network might be used to diagnose whether a patient is suffering from a mere common cold (C) and/or the more dangerous Martian Death Flu (M), based on the patients' symptoms -- whether or not the patient has a runny nose (R), whether or not the patient has a headache (H), and whether or not the patient occasionally spontaneously bursts into flames (S) -- as well as relevant background information, namely whether or not he or she has previously visited Mars (V).

Assuming all six variables are binary, with 1 representing ``true'' and 0 ``false'', the probability tables for the network might be defined as follows:

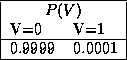
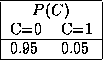
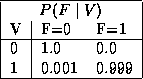
Once a Bayesian network has been specified, it may be used to compute any conditional probability one wishes to compute. For example, given that a person has recently visited Mars and has a runny nose, the network above could be used to compute the probability that the person has the common cold but not the Martian Death Flu.

Bayesian networks are very convenient for representing systems of probabilistic causal relationships. The fact ``X often causes Y'' may easily be modeled in the network by adding a directed arc from X to Y and setting the probabilities appropriately. On the other hand, if A has no causal influence on B, we may simply leave out an arc from A to B. (For example, there is no arc from C to S in the network above, since the common cold presumably neither causes nor prevents spontaneous combustion.)

Some important Bayesian network caveats / research areas :

• Calculating conditional probabilities with general Bayesian networks is NP-hard. However, there are techniques that can often make these calculations practical even with fairly large network structures.
• How does one automatically learn Bayesian networks from data?
  • In general, finding the best network structure is NP-hard; combinatorial optimization techniques such as hillclimbing or simulated annealing are often used to search for good network structures.
  • If not all the variables are observable in the data, calculating the correct probabilities to use in the probability tables can also be difficult (even when the network structure has already been fixed), typically requiring the use of iterative methods such as EM.

More Information

• Pearl, J. (1988). Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann, San Mateo, California.
• A Guide to the literature of Probabilistic Methods for Decision Support Systems (Page originally compiled by Greg F. Cooper )
• David Heckerman's tutorial on learning with Bayesian networks.

Back to Glossary Index