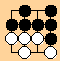
On a 4X4 board, White has just captured a Black stone in ko.
From: billspight@aol.com (BillSpight)
Newsgroups: rec.games.go
Subject: Re: Rules
Date: 6 Sep 1997 01:53:43 GMT
All:
I hope to be able to introduce something new into this discussion: the mean value and temperature of positions. There exist rationales from combinatorial game theory for determining the mean values of go positions. By their nature, mean values disregard particulars such as--in the case of ko positions--the existence of ko threats and who has the move. You can also determine the "temperature" of a position, which indicates the eagerness of players to play from it. The temperature typically equals the miai value of the plays from that position.
I think these values are relevant for two reasons.
By no means do I wish to suggest that go rules should conform to some mathematical theory. I do think, however, that that theory can shed some light on these discussions.
Without further ado, I want to give the mean values and mean temperatures
of positions discussed by Thomas Hsiang and Barry Phease. For convenience
I shall use Japanese values. [And how might these differ from any
other? -wjh]
a) 
On a 4X4 board, White has just captured a Black stone in ko.
b) 
The game has come to an end. [If no capture, by what moves? WLS]
See what I mean? This is a hot position which favors White, yet the question is whether it is jigo or Black wins by 1. White would like to play the ko, but is prevented by the rules.
c) 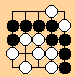
White has captured 1 Black stone.
d) 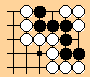
This is the upper right corner of a large board.
e) 
Also the upper right corner of a large board.
Interestingly, the theory jibes with Japanese tradition for d and e. However, it ignores ko threats, as does Japanese tradition.
f)

<<B to play, by superko alone, B can capture one of W groups!>>
g) 
White to play.
h) 
<<There are two double- ko-seki's in upper corners. Here, W cannot prove
death of the lower center B group with superko. Only Ing-2 has a way
to do it by prohibiting moves out of a cycle.>>
I don't think that Thomas Hsiang's claim that W cannot prove the death of the lower center group with is the case. With superko the double kos are not seki, but miai worth 20 points to Black. (Hence the temperature of 0.)
i) 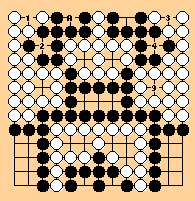
Black to play. B 5 takes ko (2). W 6 takes ko at (1). B 7 takes
ko at (4). W 8 takes ko at (2). W 10 at A, capturing the black group.
After W 10 at A, I don't think White will have any trouble taking the
lower Black group.
Now for the Barry Phease examples:

<<Here everyone agrees that "O" is dead.>>
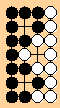
<<Here everyone agrees that "O" is dead.>>
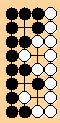
<<But here the Ing rules think it is seki. Under superko "O" is dead.
Also in Japanese rules.>>
Food for thought (I hope).
Best, Bill