Computational Photography Final
Project- Mid Project Report
E. Begum Gulsoy
Motivation: Given a set of grains such as the one below being able to extract an average shape through PCA analysis and observing how close this shape is to the commonly assumed average shape, a sphere. If possible, generating new grains using the eigen space and also using the data in exploring 3D morphing.
Limitations: The grains in a microstructure are oriented in different directions; they have to be reoriented with respect to a single axis in order to be able to make a consistent comparison in shape.Therefore, if time is not allowed I might be generating a simpler new dataset, mimicking random grain shapes but keeping the orientation information under control.
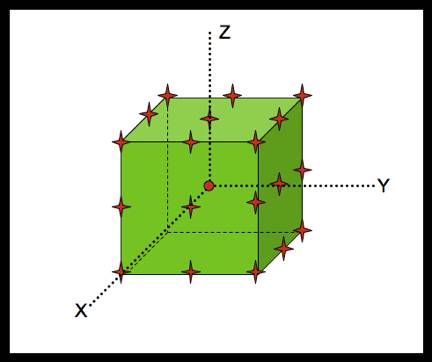
The idea: Lets assume we have two 3D shapes. For simplicity we will assume a cube and a prism.


Then, we will find the center of mass for each object. Assuming the orientation is constant we will shift one with respect to the other to create a common reference axis.

This doesnÕt feel right but we confirm that we have shifted the object the right way by looking at the consecutive layers through the 3D stack.


Since these are two very similar objects, calculating an average shape is not a problem. Keeping in mind the vertices and finding the midpoints between two corresponding vertices we are able to define an average shape.

Now that we have the basic shapes we would like to think into how we would be defining corresponding points for more complex ones. Here is the idea:
Starting from our 3D shape, defined as a binary array, we calculate a 3D distance map. Then we threshold the distance map such that only the surface voxels remain. A distance map will label the minima(the center of mass) as the maximum and the edges as the minimum such that this will mean those pixels right on the edge are the closest to the edge.

Now that we have the skeleton of our shape, using random directions from our common axis we can get corresponding pixels.
This is what IÕve got so far. One problem I am looking into is how to mesh the two shapes consistently. I can mesh the objects but the current meshing function finds the vertices itself and does not allow the user to input points therefore I still am looking for a function which will allow inputting points which are to form the vertices to be meshed ( like we did in 2D face morphing case ). Assuming I can generate a consistent triangulated mesh, another question is whether a simple affine transformation is enough for a 3D morphing case. To learn more about the subject I have done a small literature review and am currently reading those papersÉ
FINAL REPORT
Submitted: 17.12.2007
Final Paper submitted for class: EBGpaper.pdf
Taking from where I left off with the mid-project report:
How to find the corresponding directions
Here is a simplified version of the idea behind
parameterization and sampling in this project:

Starting from the center the algorithm marches in one direction that has an initial step size in x, y, z all of which have been separately and randomly generated. As can be seen in the image, not every attempt to determine a corresponding direction is successful. Yet, those who are successful provide a robust basis of corresponding points. Assuming the sampling can be made dense enough it is possible to approximate many of the complex shapes.
Once the corresponding points are defined a PCA analysis is done in order to determine the variance in the shape of the structures.
Application to simple shapes
Given two simple shapes:


We first extract their skeletons, shown below as 2D slices through the 3D object:


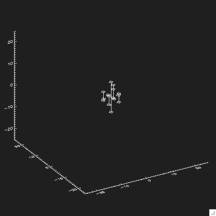
Then we pick random directions:






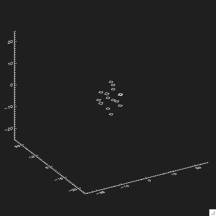
And generate the eigen vectors, where first eigen vector is:

Then we can use this eigen vector to morph fro one to the other image:


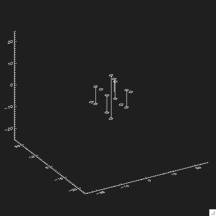
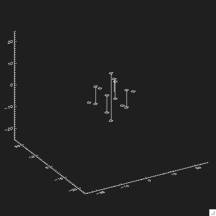



Application to Grains
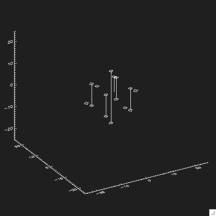
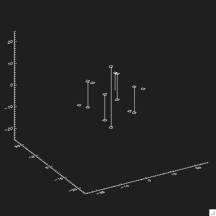
Given two grains in 3d:


We first extract their skeletons, again in 3d:


Then we pick some random and some pre-defined directions such as:
Through these points we first calculate an average shape:


 shown: the XY, YZ and XZ planes cut
through the middle
shown: the XY, YZ and XZ planes cut
through the middle
Then we run a PCA analysis and end up with 2 eigen vectors:

The first eigen vector allows for a smooth transformation from one shape into another, such that it is possible to imitate a 3D morphing effect:

Finally using the eigen vectors it is also possible to calculate new shapes that show the same characteristics as the two grains:



This project has been an attempt in observing the shape characteristics of a digitally reconstructed microstructure. Even though the results were not able to investigate this fully, the current results were concluded to be promising in achieving this aim up to a certain extent.