Fredkin automaton
A reversible cellular automaton using Fredkin's construction.
Mazoyer's firing squad
A 6-state solution to the firing squad problem due to Mazoyer.
Marxen-Buntrock busy beaver
The first 800 steps of the Marxen-Buntrock 5-state busy beaver machine.
Computing majority on a cellular automaton
A binary width 7 cellular automaton that tests majority (with high probability).
A Sierpinski gasket
A Sierpinski triangle generated by translating [3]^8 into coordinates via the
substitution 1 -> (0,0), 2 -> (0.5,1), 3 -> (1,0.2).
Towers of Hanoi
An optimal solution in the 5-disk Towers of Hanoi problem.
Log kernel
The 2-kernel of the binary digit count sequence.
Polynomial bijection
Cantor's classical bijection from N x N to N using a quadratic polynomial.
Another polynomial bijection
A bijection from N x N to N based on two quadratic polynomials.
Bitwise xor
Bitwise xor of all 6-bit numbers.
Knight moves
Up to 6 moves of a knight on an 8 by 8 chessboard.
Odd-parity cover
An odd-parity cover for the 100 by 100 grid graph.
Fibonacci rank of appearance
The involution f(x) = x + 1 acting on the Fibonacci rank of appearance of all
irrededucible polynomial of degree 8 over GF(2).
Divisor lattice
The divisor lattice of 148176 and the Hasse diagram (as Boolean matrices).
Hasse diagram
The Hasse diagram of the divisor lattice of 148176 as a directed acyclic graph.
Von Neumann ordinal 5
The von Neumann ordinal 5 in tree representation.
Von Neumann ordinal 5
The von Neumann ordinal 5 in DAG representation with shared subexpressions.
Moore automaton
A slightly nondeterministic finite state machine due to Moore that demonstrates
full exponential blow-up during deterministic simulation.
A circulant automaton
A slightly nondeterministic finite state machine based on a circulant graph
that demonstrates full exponential blow-up during deterministic simulation.
A Jiraskova automaton
A highly nondeterministic finite state machine due to Jiraskova that demonstrates
full exponential blow-up during deterministic simulation.
Canonical DFA for even 4-permutations
A DFA that recognizes all even permutations over a 4-letter alphabet.
Dihedral group action
The dihedral group D_6 acting on binary lists.
An alternating group action
The alternating group A_6 acting on binary lists.
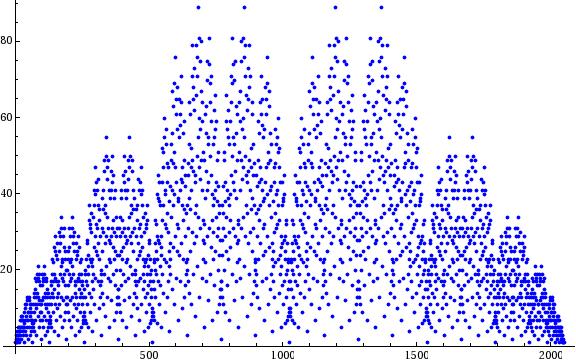
Collatz stopping time
The stopping times for the first 2048 values of the Collatz function.
Collatz on powers of 3
The up/down counts of the Collatz function for the first 100 powers of 3.
A chaotic tent map
A chaotic orbit of a transcendental point under a simple tent map.
Discret logistic map
500 steps of a 50-bit discrete version of the logistic function with parameter value 3.56.
Successor squares mod 512
The relation associating squares and squares of successors modulo 512.
Knuth-Calkin
Redundancy of 10-digit hyper-binary representations.
One-dimensional sandpile
A few steps in the evolution of a one-dimensional sandpile.
The devil's staircase
A monotonic function on the unit interval such that f(0) = 0, f(1-x) = 1 - f(x)
and f(x/3) = f(x)/2.
Wild surjection.
A rather bizarre surjection from the integers to the rationals:
With[ {nn = Ceiling[Sqrt[n]]},
If[ n ≤ (nn-1)^2 + nn, nn/(n - (nn-1)^2), (nn^2 - n + 1)/nn ]]
Farey and Ford
The Farey sequence and Ford circles.
Conway's T function
The first 250 points in the backward and forward orbit of 8 under Conway's T
function (log-lin plot).
Iterating the 1/2 operator
The number of predecessors under the operation f(n) = n/2 using ceilings and floors.
Riffle shuffle
A complete orbit under riffle shuffle.
Isomorphs
Domino tilings equivalent under rotation and reflection.
Necklaces
All 4-colored necklaces of length 5, in canonical order.
Stack turtle curve
A polygonal curve generated by a stack turtle.
Stack turtle rug
A fractal rug generated by a stack turtle.
 © 2023 K. Sutner
© 2023 K. Sutner
Last modified: 2023/04/17
 Computation & Discrete Math
Computation & Discrete Math